ndvi_diff = ndvi2023_tartu - ndvi2018_tartu
plot(ndvi_diff)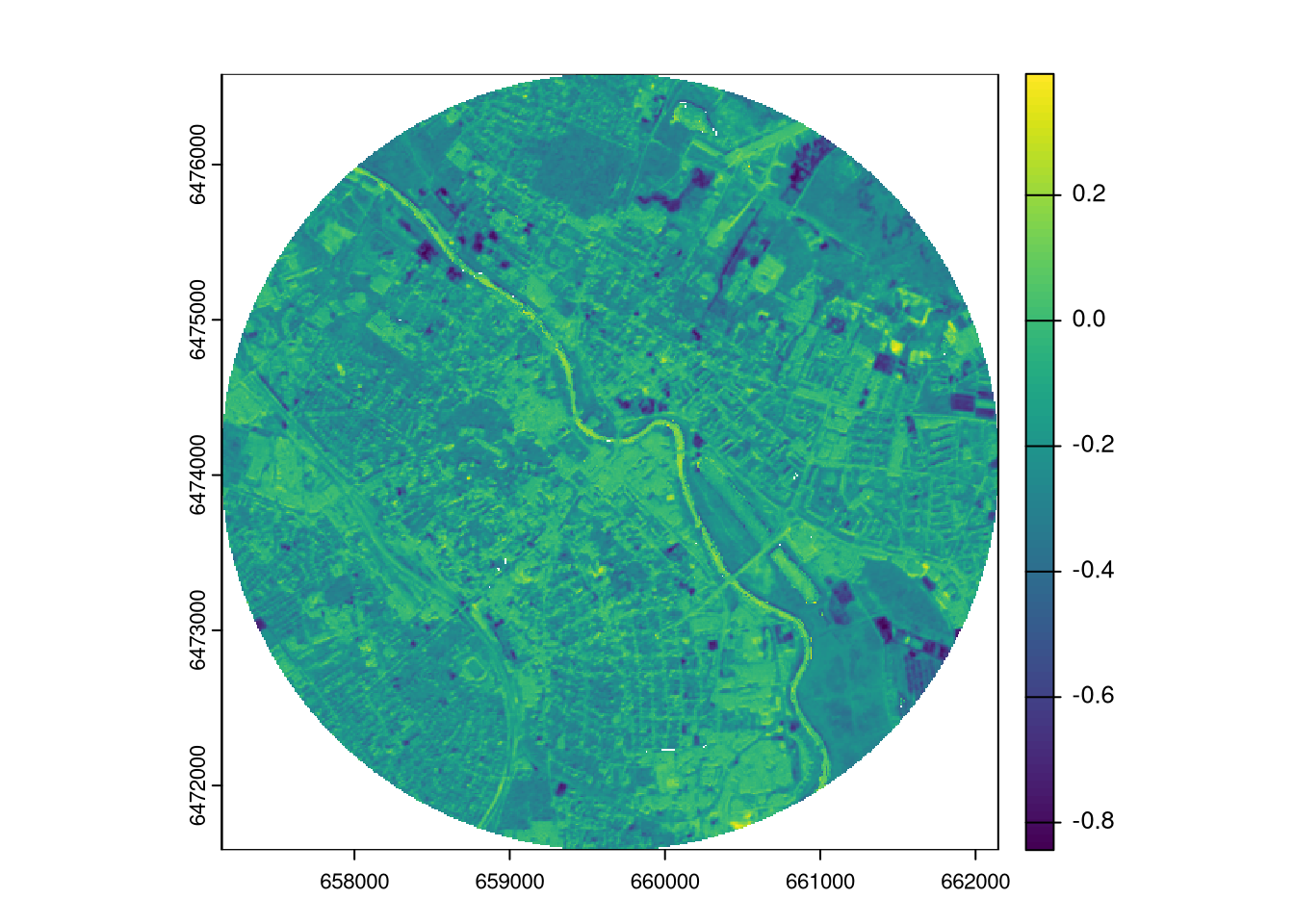
October 20, 2024
This is the second part of a blog post series on comparing spatial patterns in raster data. More information about the whole series can be found in part one.
This blog post shows various methods for comparing spatial patterns in continuous raster data for overlapping regions, i.e., how to compare two rasters for the same region, but in different moments in time (or, in some cases, with different variables)1 using R programming language.
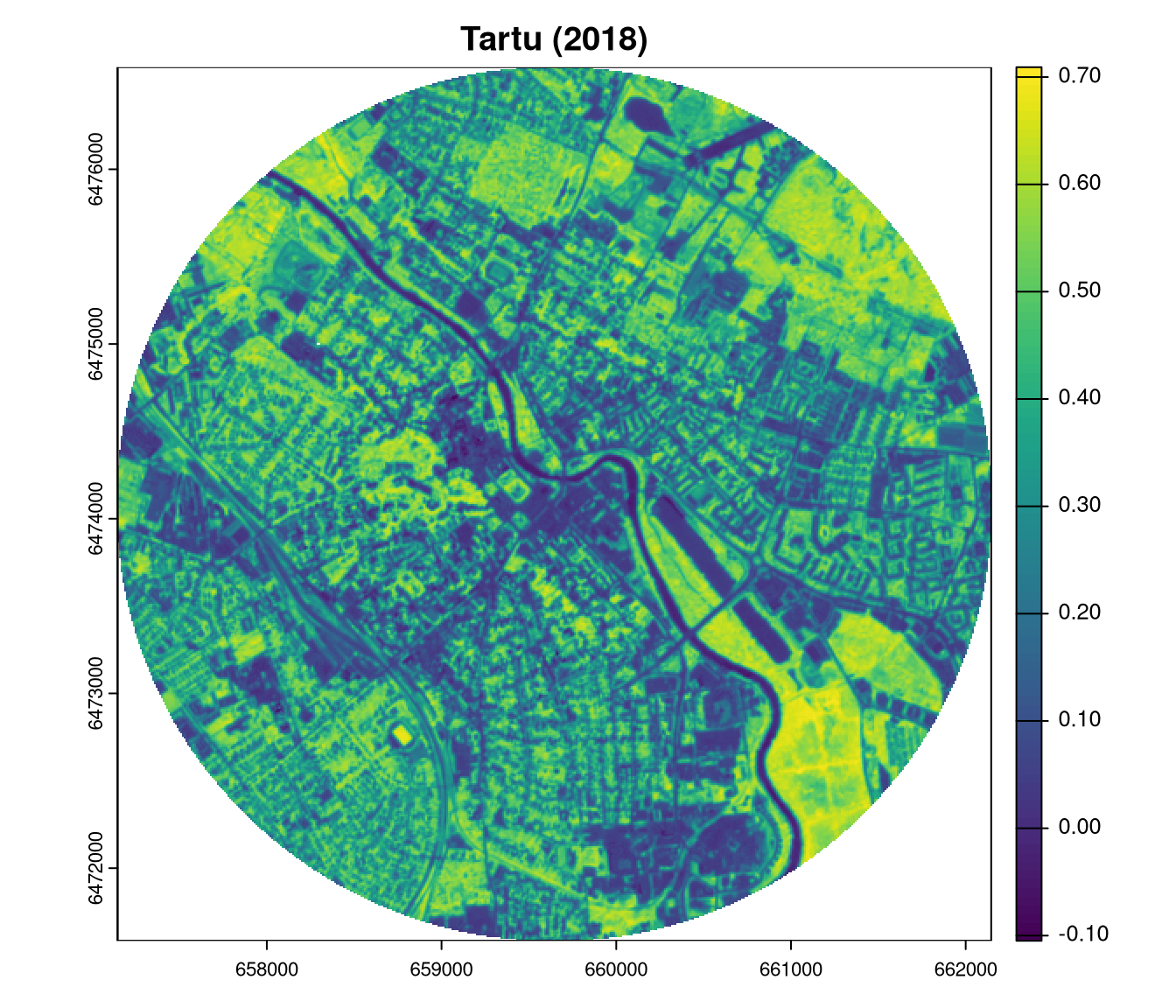
Two continuous raster datasets are used in this blog post: the Normalized Difference Vegetation Index (NDVI) for Tartu (Estonia) for the years 2000 and 2018.
library(terra)
ndvi2018_tartu = rast("https://github.com/Nowosad/comparing-spatial-patterns-2024/raw/refs/heads/main/data/ndvi2018_tartu.tif")
ndvi2023_tartu = rast("https://github.com/Nowosad/comparing-spatial-patterns-2024/raw/refs/heads/main/data/ndvi2023_tartu.tif")
plot(ndvi2018_tartu, main = "Tartu (2000)")
plot(ndvi2023_tartu, main = "Tartu (2018)")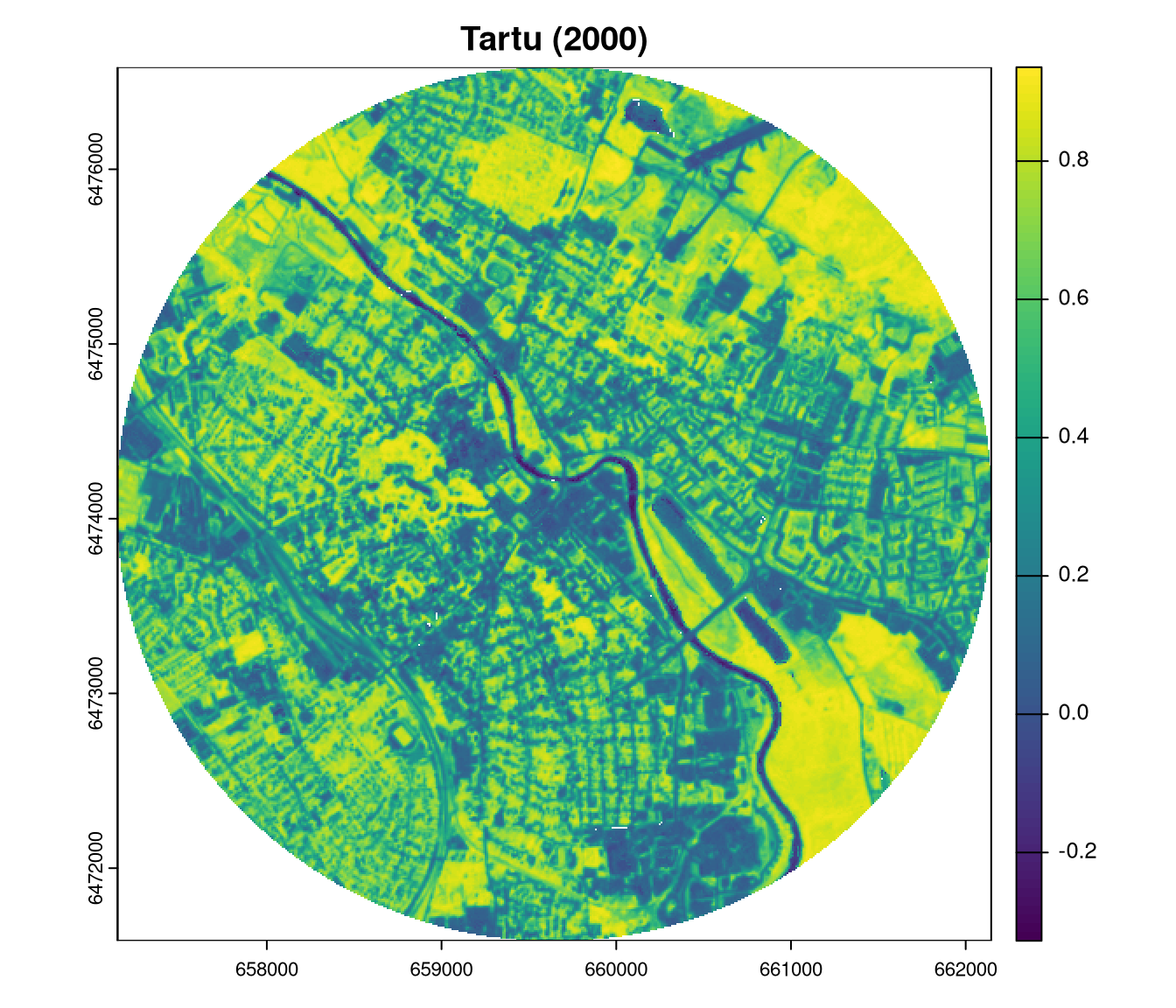
The most basic approach to compare two continuous rasters is to calculate the difference between their values for each cell.
The output is a raster with positive values indicating that the values of the first raster are higher than the values of the second raster, while negative values indicate the opposite.2
The differences may be even more highlighted by using a diverging color palette. The below function plot_div() visualizes a raster with a diverging color palette, where the middle color represents zero.
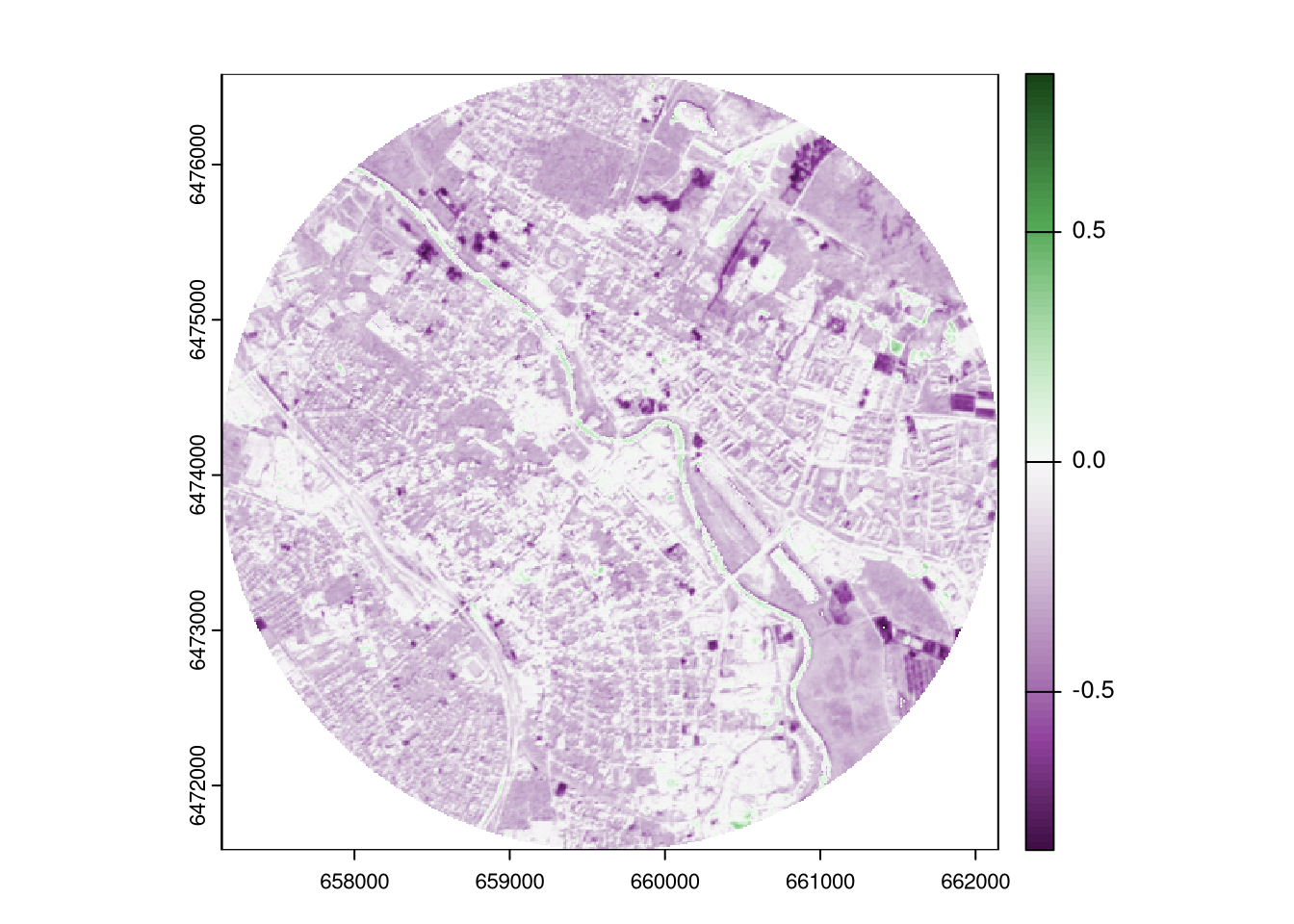
It shows that most of the area has negative values, indicating that the NDVI values were lower in 2023 than in 2018.
The interpretation of the difference between the values of two rasters is not always straightforward as it depends, among other things, on the properties of the studied variable. Some variables are linear, and thus, the difference between the values has a clear meaning, while others are not, and the difference may be harder to interpret.3
A similar approach, also based on the values of each cell independently, is to calculate the statistics of the differences between the two rasters’ values (i.e., error metrics).
One of the most common error metrics is the Root Mean Square Error (RMSE), which quantifies the average difference between the values of the two rasters. Its lower value indicates a better agreement between the two rasters. RMSE is implemented in many R packages, and here we use the version from the yardstick package (Kuhn, Vaughan, and Hvitfeldt 2024).4
In general, error metrics require two sets of values; thus, we are using the values() function to extract the values of the rasters before calculating the RMSE.
[1] 0.2191853The diffeR package (Pontius Jr. and Santacruz 2023), on the other hand, is directly aimed at comparing rasters. One of its functions, MAD(), calculates the Mean Absolute Difference (MAD) between two rasters.
[1] "The mean of grid1 is less than the mean of grid2"[1] 0.184306This measure has a similar interpretation to RMSE, but it is less sensitive to outliers.
The main general approach of incorporating spatial context into comparison of rasters is the use of calculations in a moving window. This way, we do not only consider the values of each cell independently, but also the values of the surrounding cells.5
The focalPairs() function from the terra package (Hijmans 2024) uses a moving window to extract values from the focal regions of two rasters and calculates the correlation coefficient between them. It requires two rasters with the same number of rows and columns, the size of the moving window, and the function to calculate the correlation coefficient.6
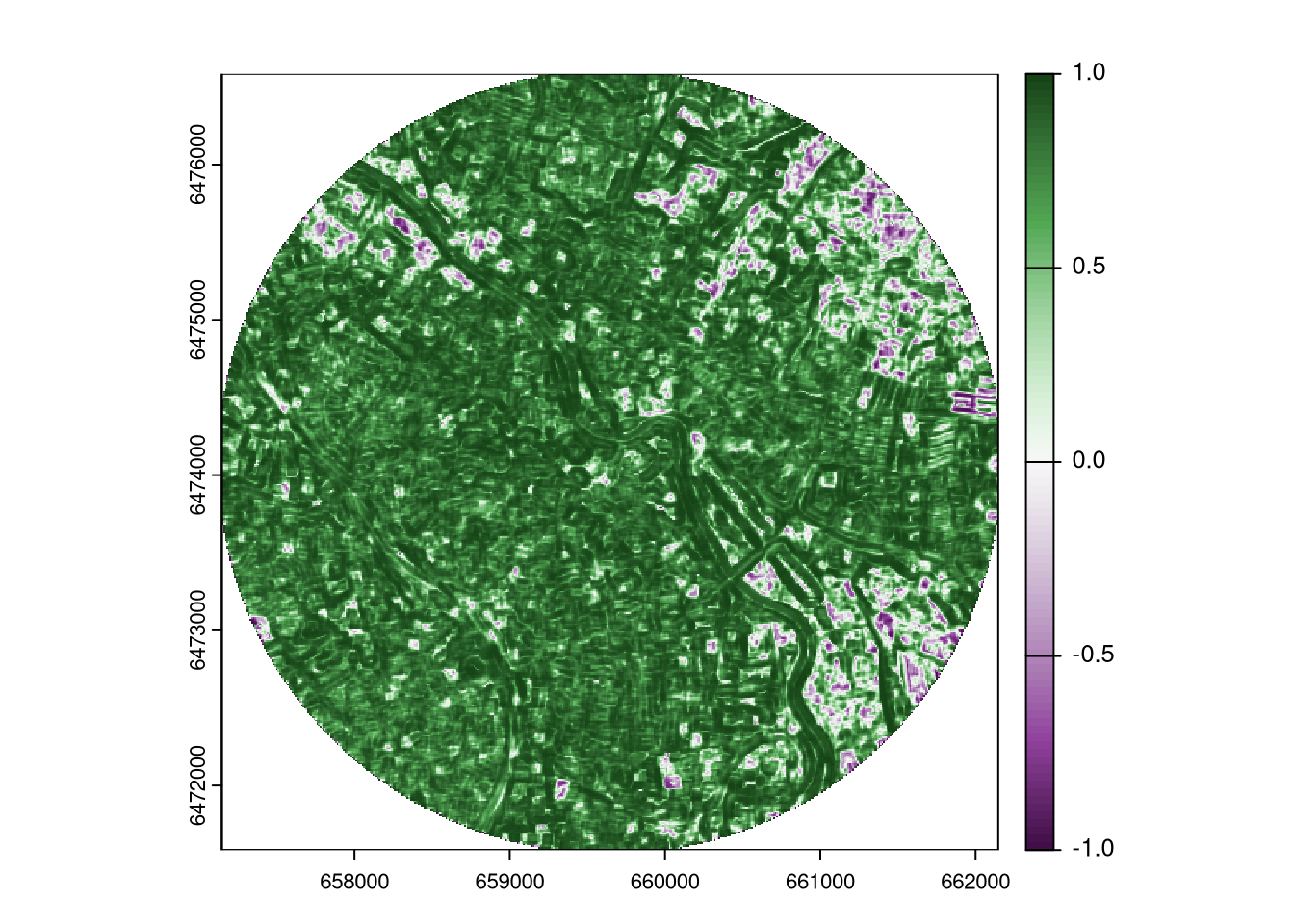
The values of the output raster range from -1 to 1, where 1 indicates a perfect positive correlation in the focal regions, 0 indicates no correlation (the focal values have no relationship to each other), and -1 indicates a perfect negative correlation.
Similarly to the correlation coefficient, other statistics can be calculated in a moving window. This option is offered by several R packages, including geodiv (Smith et al. 2023), GLCMTextures (Ilich 2020), and rasterdiv (Rocchini et al. 2021).
The geodiv package provides a function focal_metrics() that calculates more than 20 different focal statistics. In the below example, we calculate the average surface roughness (SA) in a moving window separately for the two rasters and then calculate the difference between them.
library(geodiv)
window = matrix(1, nrow = 5, ncol = 5)
ndvi2018_tartu_sa_mw = focal_metrics(ndvi2018_tartu, window = window,
metric = "sa", progress = FALSE)
ndvi2023_tartu_sa_mw = focal_metrics(ndvi2023_tartu, window = window,
metric = "sa", progress = FALSE)
ndvi_diff_sa_mw = ndvi2023_tartu_sa_mw$sa - ndvi2018_tartu_sa_mw$sa
plot_div(ndvi_diff_sa_mw)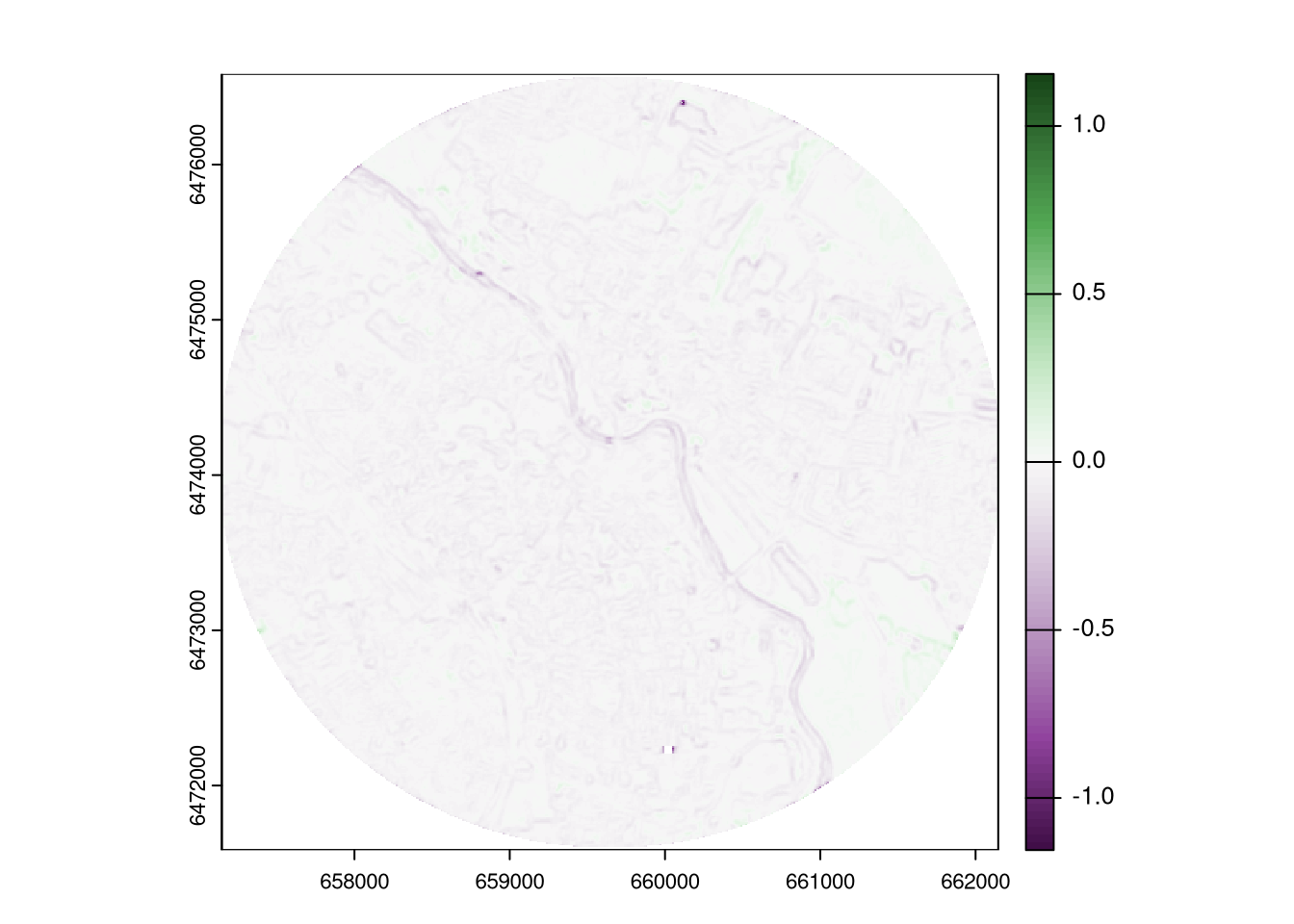
This outcome shows the difference in the average surface roughness between the two rasters in a moving window. The possitive values indicate that the surface roughness (in this case, the heterogeneity of NDVI) was higher in 2023 than in 2018, while the negative values indicate the opposite. Interestingly, the most extreme (negative) values are located in just a few small areas.
We can also compare various texture GLCM (Gray-Level Co-occurrence Matrix) metrics (Haralick, Shanmugam, and Dinstein 1973) in a moving window that characterizes many aspects of the spatial structure of the rasters. This example uses the GLCMTextures package (Ilich 2020). We calculate the homogeneity of the NDVI values in a moving window for both rasters and calculate the difference between them.
The positive values in the resulting map indicate that the homogeneity of the NDVI values was higher in 2023 than in 2018, while the negative values indicate the opposite.
The Rao’s quadratic entropy is a measure of diversity that takes into account not only the abundance of the classes (values), but also the dissimilarity between them (Rao 1982).
This measure can be calculated using the paRao() function from the rasterdiv package (Rocchini et al. 2021). The function requires the raster with integer values (thus we multiply the NDVI values by 100) and the size of the moving window.
library(rasterdiv)
ndvi2018_tartu_int = as.int(ndvi2018_tartu * 100)
ndvi2023_tartu_int = as.int(ndvi2023_tartu * 100)
ndvi2018_tartu_rao = paRao(ndvi2018_tartu_int, window = 5, progBar = FALSE)
ndvi2023_tartu_rao = paRao(ndvi2023_tartu_int, window = 5, progBar = FALSE)
ndvi_rao_diff = ndvi2023_tartu_rao[[1]][[1]] - ndvi2018_tartu_rao[[1]][[1]]
plot_div(ndvi_rao_diff)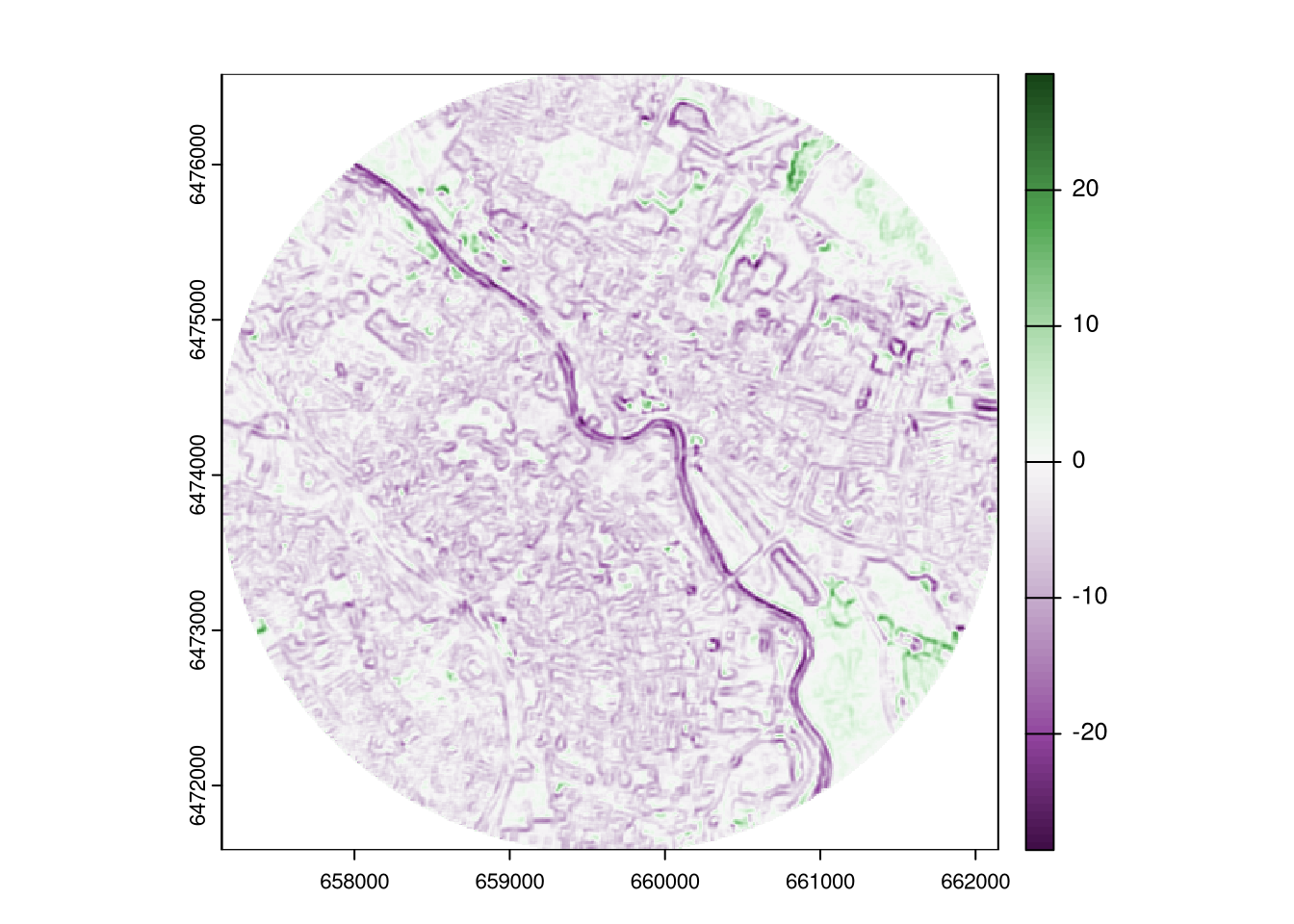
Note that the above calculations may take a few minutes to complete.
The positive values in the resulting map indicate that the diversity (in this case, the heterogeneity of NDVI) was higher in 2023 than in 2018, while the negative values indicate the opposite.
An alternative approach for computing metrics in two rasters and then calculate the difference between them is to calculate the difference between the two rasters, and then compute the spatial autocorrelation of the differences (Cliff 1970).
The terra package provides a function autocor() that calculates the spatial autocorrelation of a raster using a selected method. By default, it uses a three by three moving window (excluding the focal cell) to calculate the Moran’s I index. The global = FALSE argument specifies that the spatial autocorrelation should be calculated for each cell separately, and thus the output is a raster.
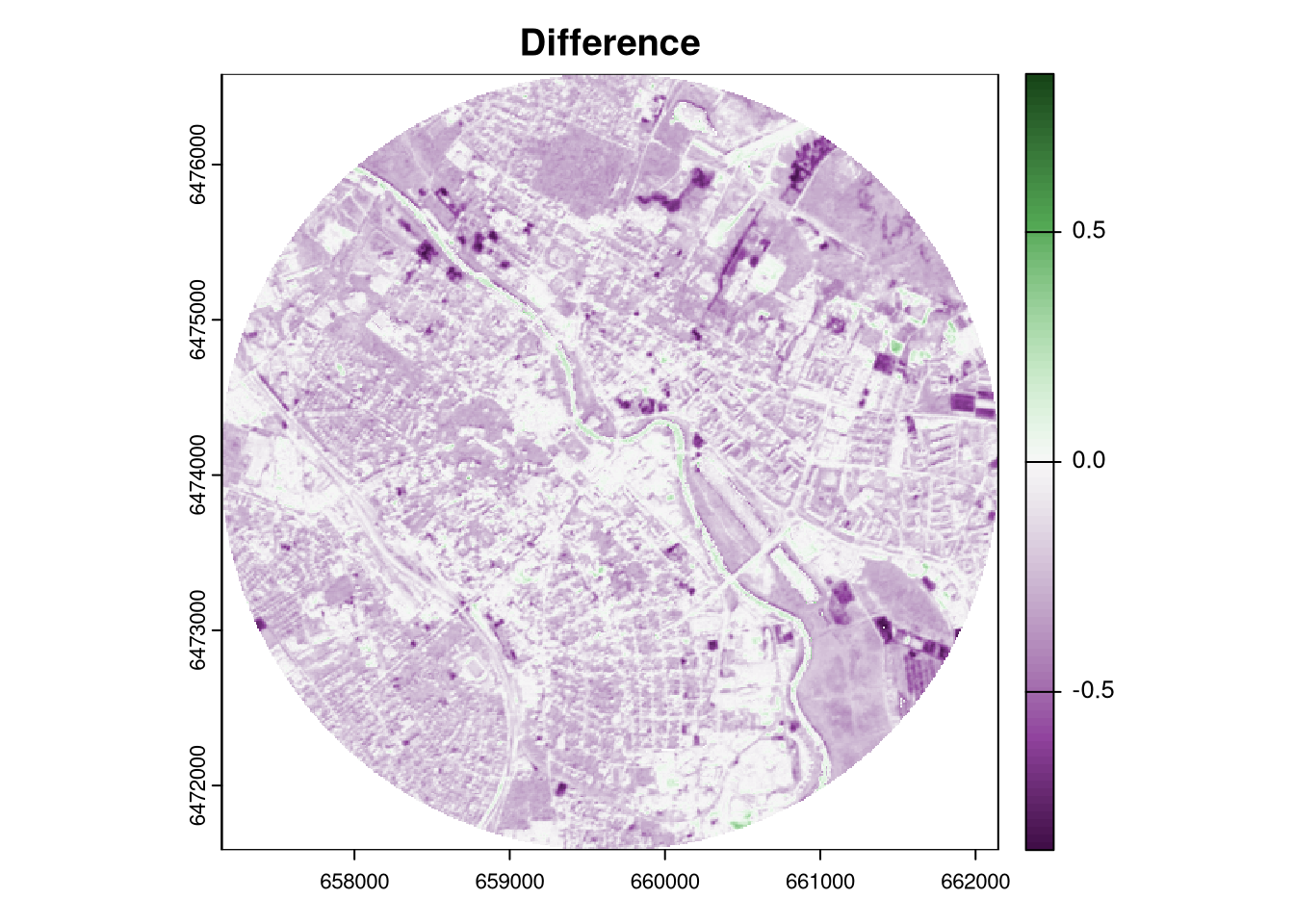
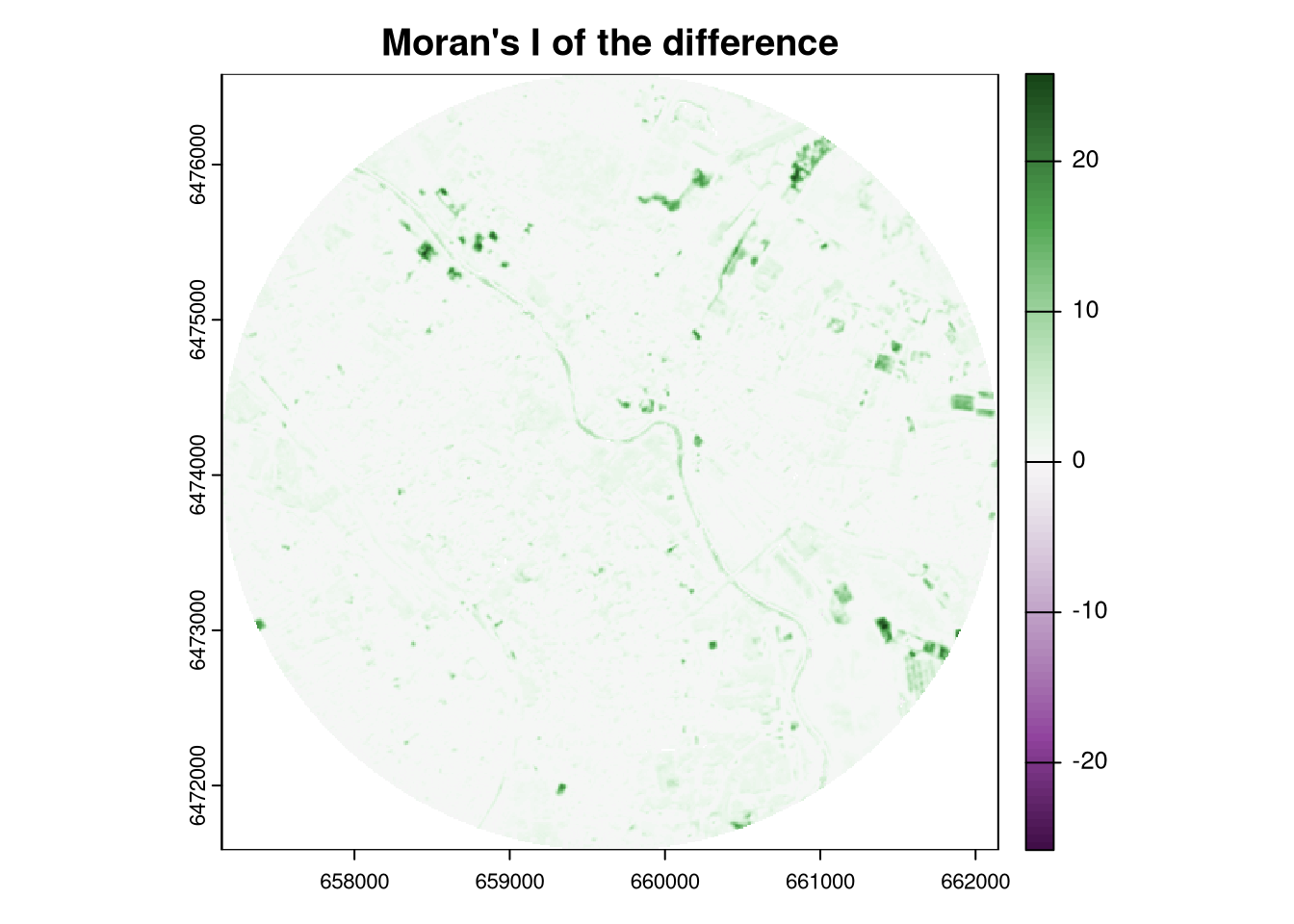
The resulting map shows the spatial autocorrelation of the differences between the two rasters. Its high values indicate that the differences are spatially clustered (positive changes are close to positive changes, and negative changes are close to negative changes), while low values indicate that the differences are spatially random. Areas with no spatial autocorrelation (values around zero) indicate that the differences are spatially independent.
Structural similarity index (SSIM) (Wang et al. 2004) is a measure used to compare similarity between two images (no surprises here). It is based on the comparison of three aspects of the images: luminance, contrast, and structure, and its idea is to mimic the human perception of similarity.
The SSIMmap package (Ha and Long 2023) provides a function ssim_raster() that calculates the SSIM between two rasters.7
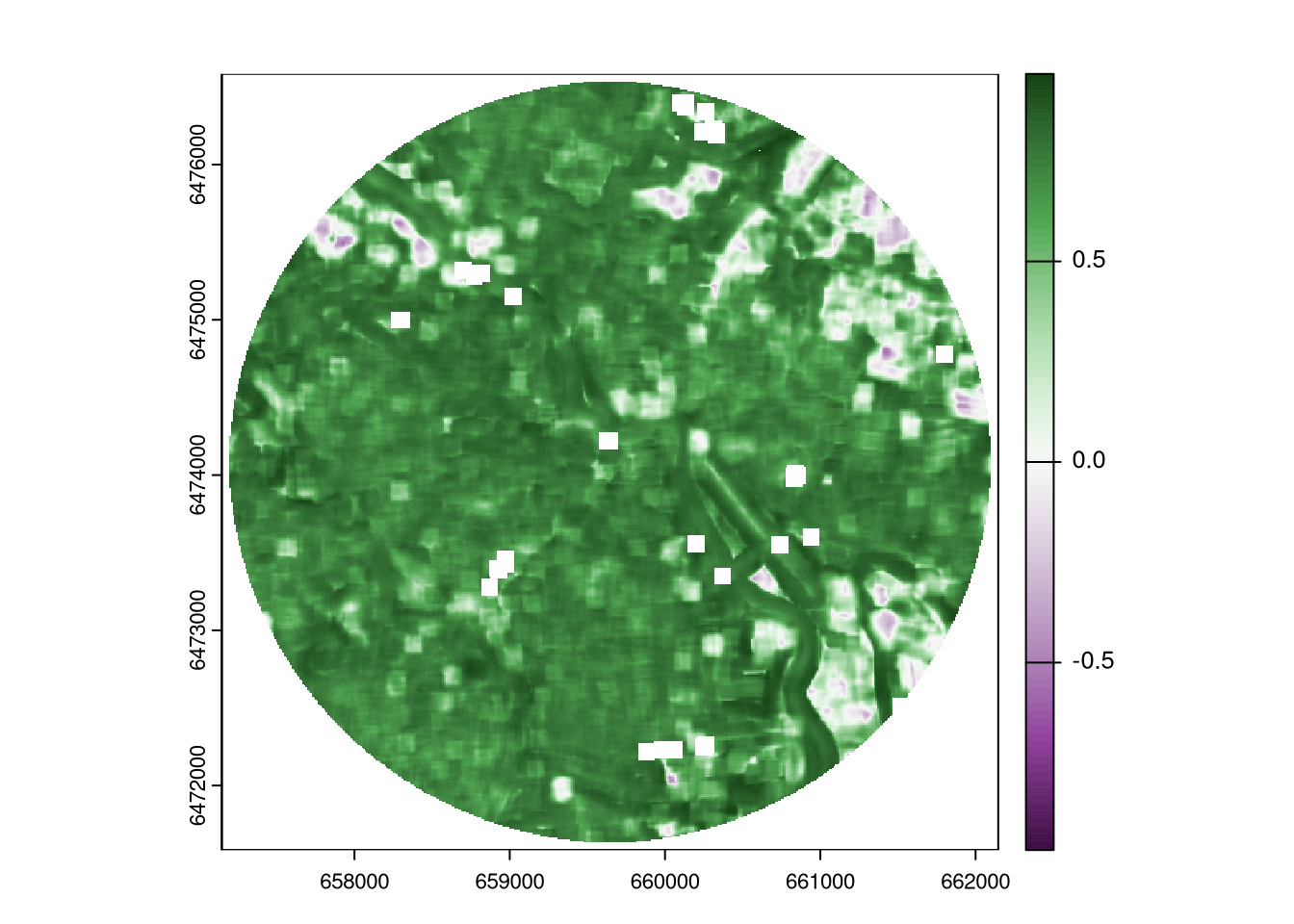
The interpretation of the SSIM values is similar to the correlation coefficient: 1 indicates a perfect similarity, 0 indicates no similarity, and -1 indicates a perfect dissimilarity.
As of writing this blog post, the results from the SSIMmap package seem not to be consistent with other R implementations of SSIM. See https://github.com/Hailyee-Ha/SSIMmap/issues/1 for more information.
All of the single value outcomes can be also calculated at multiple scales, i.e., instead of using each original cell value, the values are aggregated in windows of different sizes.
We have already seen the use of RMSE to compare two rasters based on the values of each cell independently. Now, using the waywiser package (Mahoney 2023), we can calculate the RMSE at multiple scales.
Its function ww_multi_scale() requires the two rasters, the metrics to calculate, and the sizes of the windows (in cells) to aggregate the values. Here, we calculate the RMSE at six different scales, from 50 to 300 meters (map units).
# A tibble: 6 × 6
.metric .estimator .estimate .grid_args .grid .notes
<chr> <chr> <dbl> <list> <list> <list>
1 rmse standard 0.205 <tibble [1 × 1]> <sf [10,000 × 5]> <tibble>
2 rmse standard 0.198 <tibble [1 × 1]> <sf [2,500 × 5]> <tibble>
3 rmse standard 0.195 <tibble [1 × 1]> <sf [1,156 × 5]> <tibble>
4 rmse standard 0.193 <tibble [1 × 1]> <sf [625 × 5]> <tibble>
5 rmse standard 0.193 <tibble [1 × 1]> <sf [400 × 5]> <tibble>
6 rmse standard 0.193 <tibble [1 × 1]> <sf [289 × 5]> <tibble>This result (note the .estimate column) shows the RMSE values at each scale: the largest value is at the scale of 50 meters, and the smallest value is at the scale of 200, 250, and 300 meters. It indicates that with the increase of the scale, the agreement between the two rasters increases.
A similar approach can be found in the MAD() function from the diffeR package, which calculates the Mean Absolute Difference (MAD) between two rasters at multiple scales. Here, these scales start at the original resolution of the rasters and increase by a factor of 2.
[1] "The mean of grid1 is less than the mean of grid2" Multiples Resolution Quantity Strata Element Total
1 1 10 0.1783152 0 0.0059907211 0.1843060
2 2 20 0.1783152 0 0.0038461843 0.1821614
3 4 40 0.1783152 0 0.0016917875 0.1800070
4 8 80 0.1783152 0 0.0003588876 0.1786741
5 16 160 0.1783152 0 0.0001143444 0.1784296
6 32 320 0.1783152 0 0.0001143444 0.1784296
7 64 640 0.1783152 0 0.0000000000 0.1783152
8 128 1280 0.1783152 0 0.0000000000 0.1783152
9 256 2560 0.1783152 0 0.0000000000 0.1783152
10 512 5120 0.1783152 0 0.0000000000 0.1783152Note the last column of the result, which shows the MAD values at each scale. It is similar to the RMSE result, with the largest value at the original resolution of the rasters and the smallest value at the largest scale.
The average (global) SSIM value can be calculated by averaging the SSIM values of all cells in the raster. It is a single value that indicates the overall similarity between the two rasters (Wang et al. 2004; Robertson et al. 2014).
It can be calculated using the ssim_raster() function from the SSIMmap package(Ha and Long 2023).
SSIM: 0.63845 SIM: 0.90432 SIV: 0.90778 SIP: 0.75671 The result is a single value that ranges from -1 to 1, where 1 indicates a perfect similarity, 0 indicates no similarity, and -1 indicates a perfect dissimilarity.
As of writing this blog post, the results from the SSIMmap package seem not to be consistent with other R implementations of SSIM. See https://github.com/Hailyee-Ha/SSIMmap/issues/1 for more information.
In fact, they may also be used for comparing rasters for other regions, but they still should have the same number of rows and columns.↩︎
Alternatively, the absolute difference can be calculated to show the difference in the magnitude of the values.↩︎
Read the comment on this by Mathieu Gravey.↩︎
Implementation of RMSE is also straightforward: rmse = function(x, y) sqrt(mean((x - y)^2)).↩︎
This leaves a tough question of how to choose the size of the moving window.↩︎
The “pearson” method is the only one available by name, but other methods can be used by providing a custom function.↩︎
This function also returns three other rasters: SIM, SIV, and SIP that relate to the luminance, contrast, and structure, respectively.↩︎
@online{nowosad2024,
author = {Nowosad, Jakub},
title = {Comparison of Spatial Patterns in Continuous Raster Data for
Overlapping Regions Using {R}},
date = {2024-10-20},
url = {https://jakubnowosad.com/posts/2024-10-20-spatcomp-bp2/},
langid = {en}
}