3 Przetwarzanie macierzy

3.1 Tablice

Informacja w pamięci komputera przypisana do zmiennej może być przechowywana w formie pojedynczego obiektu (niezależnie od stopnia złożoności) lub w formie tablicy (ang. array) obiektów tego samego typu. Tablica jest podstawowym typem służącym do przechowywania takich struktur, niezależnie od języka programowania.

Jeżeli tablica jest jednowymiarowa, to znaczy zawiera ciąg obiektów, na przykład liczb, znaków lub innych obiektów określana jest z reguły jako wektor (ang. vector). Dwuwymiarowa struktura określona jest jako macierz (ang. matrix), a tablica posiadająca trzy i więcej wymiarów określana jest terminem tensor.

3.1.1 Wektory

Wektor to ciąg wartości, które mogą być przechowywane w jednym wymiarze. Wektor może być reprezentowany jako ciąg wartości liczbowych, znakowych lub innych obiektów. Często wektory są stosowane jako kolumny w bazach danych, atrybuty w obiektach wektorowych, itp. Główną właściwością wektora jest to, że posiada długość, czyli liczbę elementów.

R
Python

vec = c(1, 2, 3)
vec

[1] 1 2 3

import numpy as np
vec = np.array([1, 2, 3])
vec

array([1, 2, 3])

3.1.2 Macierze

Macierz to dwuwymiarowa struktura danych, w której wartości są zorganizowane w wierszach i kolumnach. Macierz może być reprezentowana jako tablica dwuwymiarowa, gdzie każda wartość jest tego samego typu. Macierze mogą być stosowane do przechowywania danych tabelarycznych, obrazów, danych rastrowych (jeden kanał/warstwa), itp.

R
Python

mat = matrix(c(1, 2, 3, 4, 5, 6), nrow = 2)
mat

     [,1] [,2] [,3]
[1,]    1    3    5
[2,]    2    4    6

import numpy as np
mat = np.array([[1, 2, 3], [4, 5, 6]])
mat

array([[1, 2, 3],
       [4, 5, 6]])

Macierze mają także szerokie zastosowanie w różnorodnych operacjach matematycznych, na przykład w analizie danych, statystyce, analizie obrazów. Macierze mogą być też używane do przechowywania przestrzennych danych rastrowych. Przykładami często stosowanych macierzy są macierze odległości, kowariancji, czy korelacji.

Macierze są specyficzną formą tablic o dwóch wymiarach. Jeżeli język programowania nie definiuje macierzy jako osobnego typu danych, operacje algebraiczne na macierzach są realizowane w sposób właściwy dla tablic, tj. element po elemencie. Operacje właściwe dla rachunku macierzowego, na przykład mnożenie macierzy, jest realizowane dedykowanymi operacjami.

Przykład macierzy korelacji:

R
Python

gm = readr::read_csv("data/gapminder_1950_2023.csv")
gm2000 = subset(gm, Rok == 2000)
cor(gm2000[, 4:8], use = "pairwise.complete.obs")

                Populacja PKB_na_osobe Ocz_dl_zycia CO2_na_osobe    Plodnosc
Populacja     1.000000000  -0.08007049  0.005225497  -0.04998688 -0.08035338
PKB_na_osobe -0.080070492   1.00000000  0.589105273   0.77303757 -0.52478608
Ocz_dl_zycia  0.005225497   0.58910527  1.000000000   0.44145140 -0.81239019
CO2_na_osobe -0.049986876   0.77303757  0.441451403   1.00000000 -0.42379885
Plodnosc     -0.080353380  -0.52478608 -0.812390192  -0.42379885  1.00000000

import pandas as pd
gm = pd.read_csv("data/gapminder_1950_2023.csv")
gm2000 = gm[gm["Rok"] == 2000]
gm2000.iloc[:, 3:8].corr()

              Populacja  PKB_na_osobe  Ocz_dl_zycia  CO2_na_osobe  Plodnosc
Populacja      1.000000     -0.080070      0.005225     -0.049987 -0.080353
PKB_na_osobe  -0.080070      1.000000      0.589105      0.773038 -0.524786
Ocz_dl_zycia   0.005225      0.589105      1.000000      0.441451 -0.812390
CO2_na_osobe  -0.049987      0.773038      0.441451      1.000000 -0.423799
Plodnosc      -0.080353     -0.524786     -0.812390     -0.423799  1.000000

3.1.3 Tensory

Tensor to struktura danych, która może przechowywać dane o dowolnej liczbie wymiarów. Tensor jest zazwyczaj reprezentowany jako tablica wielowymiarowa, gdzie każda wartość jest tego samego typu.

R
Python

tensor = array(1:27, dim = c(3, 3, 3))
tensor

, , 1

     [,1] [,2] [,3]
[1,]    1    4    7
[2,]    2    5    8
[3,]    3    6    9

, , 2

     [,1] [,2] [,3]
[1,]   10   13   16
[2,]   11   14   17
[3,]   12   15   18

, , 3

     [,1] [,2] [,3]
[1,]   19   22   25
[2,]   20   23   26
[3,]   21   24   27

import numpy as np
tensor = np.array([[[1, 2, 3], [4, 5, 6], [7, 8, 9]], [[10, 11, 12], [13, 14, 15], [16, 17, 18]], [[19, 20, 21], [22, 23, 24], [25, 26, 27]]])
tensor

array([[[ 1,  2,  3],
        [ 4,  5,  6],
        [ 7,  8,  9]],

       [[10, 11, 12],
        [13, 14, 15],
        [16, 17, 18]],

       [[19, 20, 21],
        [22, 23, 24],
        [25, 26, 27]]])

W R wartości są najpierw przypisywane wierszami, a następnie kolumnami, w Pythonie wartości są przypisywane wierszami, a następnie kolumnami.

Tensory są stosowane do przechowywania danych wielowymiarowych, takich jak obrazy wielokanałowe (np. trójwymiarowe dane rastrowe z wieloma kanałami/warstwami), filmy (np. czterowymiarowe dane w postaci klatek, kanałów, wierszy i kolumn), serie danych (np. czterowymiarowe dane w postaci stanów, warstw, wierszy i kolumn). Tensory są również szczególnie wykorzystywane w uczeniu głębokim (ang. deep learning).

3.2 Skalar a tablica

W przypadku pojedycznej wartości, wchodzącej w interakcję z obiektami tablicowymi, określa się ją w żargonie jako skalar (w nawiązaniu do rachunku macierzowego). Tablica jednoelementowa nie jest skalarem, ponieważ może mieć więcej niż jeden wymiar.

R
Python

c(1)

[1] 1

matrix(1)

     [,1]
[1,]    1

array(1, dim = c(1, 1, 1))

, , 1

     [,1]
[1,]    1

import numpy as np
np.array([1]) # 1 wymiar

array([1])

np.array([[1]]) # 2 wymiary, jeden zwinięty

array([[1]])

np.array([[[1]]]) # 3 wymiary, dwa zwiniąte

array([[[1]]])

3.3 Reprezentacja macierzy w pamięci komputera a wymiarowość tablicy

W pamięci komputera wielowymiarowa tablica reprezentowana jest jako ciąg obiektów poukładanych jeden po drugim. Natomiast dla wygody użytkownika taki obiekt może posiadać wymiarowość (ang., dimensionality). Dla różnych narzędzi stosowane są terminy, takie jak:

R: matrix/array – dimensionality
Python: numpy.array (ndarray) – shape
Macierz jako struktura danych, np. w języku C: order

W języku Python istnieje struktura danych array (nie mylić z numpy.array), która w praktyce nie jest stosowana.

Wymiarowość tablicy można swobodnie zmieniać, bez wpływania na zmianę organizacji danych w pamięci.

\[ \begin{bmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \end{bmatrix} \longmapsto \begin{bmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \end{bmatrix} \longmapsto \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \\ 7 & 8 \end{bmatrix} \]

R
Python

mat = matrix(1:8, nrow = 1)
mat

     [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,]    1    2    3    4    5    6    7    8

dim(mat)

[1] 1 8

dim(mat) = c(2, 4)
mat

     [,1] [,2] [,3] [,4]
[1,]    1    3    5    7
[2,]    2    4    6    8

dim(mat) = c(4, 2)
mat

     [,1] [,2]
[1,]    1    5
[2,]    2    6
[3,]    3    7
[4,]    4    8

import numpy as np
mat = np.array([1, 2, 3, 4, 5, 6, 7, 8])
mat

array([1, 2, 3, 4, 5, 6, 7, 8])

mat.shape

(8,)

mat.shape = (2, 4)
mat

array([[1, 2, 3, 4],
       [5, 6, 7, 8]])

mat.shape = (4, 2)
mat

array([[1, 2],
       [3, 4],
       [5, 6],
       [7, 8]])

3.4 Organizacja danych w tablicach

W tablicach dwu- i więcej wymiarowych dane jednego typu zorganizowane są liniowo, jako ciąg wartości. Pierwszy wymiar tablicy wskazuje na główne jednostki danych, a każdy kolejny na podjednostki w obrębie jednostek wyższego rzędu. Proces indeksowania tablic tym samym odwołuje się do kolejnych jednostek organizacji danych.

W przypadku tablicy dwuwymarowej, dane są zorganizowane w obrębie wierszy i kolumn. Jednostką nadrzędną jest wiersz i kolejne wartości w wierszu odnoszą są indeksowane jako numery kolumn. W przypadku danych trójwymiarowych dane zorganizowane są w postaci stosu (ang. stack) macierzy, gdzie jeden z wymiarów odpowiada poziomowi macierzy na stosie, a dwa pozostałe wymiary odpowiadają wierszom i kolumnom w każdej macierzy. Konkretna organizacja danych w tablicy zależy od implementacji języka programowania.

R
Python

tensor

, , 1

     [,1] [,2] [,3]
[1,]    1    4    7
[2,]    2    5    8
[3,]    3    6    9

, , 2

     [,1] [,2] [,3]
[1,]   10   13   16
[2,]   11   14   17
[3,]   12   15   18

, , 3

     [,1] [,2] [,3]
[1,]   19   22   25
[2,]   20   23   26
[3,]   21   24   27

tensor[1, , ]

     [,1] [,2] [,3]
[1,]    1   10   19
[2,]    4   13   22
[3,]    7   16   25

tensor[, 1, ]

     [,1] [,2] [,3]
[1,]    1   10   19
[2,]    2   11   20
[3,]    3   12   21

tensor[, , 1]

     [,1] [,2] [,3]
[1,]    1    4    7
[2,]    2    5    8
[3,]    3    6    9

tensor

array([[[ 1,  2,  3],
        [ 4,  5,  6],
        [ 7,  8,  9]],

       [[10, 11, 12],
        [13, 14, 15],
        [16, 17, 18]],

       [[19, 20, 21],
        [22, 23, 24],
        [25, 26, 27]]])

tensor[0, :, :]

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

tensor[:, 0, :]

array([[ 1,  2,  3],
       [10, 11, 12],
       [19, 20, 21]])

tensor[:, :, 0]

array([[ 1,  4,  7],
       [10, 13, 16],
       [19, 22, 25]])

W przypadku tensorów posiadających więcej niż trzy wymiary organizacja danych również nie jest oczywista. Na przykład w przypadku modelu czterowymiarowego zawierającego kolekcję obrazów lub film (klatka, warstwa koloru, wiersz, kolumna), najczęściej stosuje się dwa modele:

ncrc (number, color, row, column): kolekcja obrazów
nrcc (number, row, column, color): tensor

W pierwszym przpadku każdy obiekt (n) posiada kanały informacji (color), a w każdym kanale informacji jest dwuwymiarowa macierz. Jest to sposób właściwy dla obrazów. W drugim przypadku każdy obiekt (n) posiada topologię danych (row x col), gdzie na przecięciu wiersza i kolumny mamy komórkę zawierającą wektor cech. W przypadku obrazu będzie to trójka: (r,g,b), w przypadku danych GIS lub teledetekcyjnych, wektor cech może być, i z reguły będzie, dłuższy.

3.5 Rachunek macierzowy

Podstawowymi operacjami w rachunku macierzowym są:

Dodawanie i odejmowanie macierzy
Mnożenie macierzy
Inwersja macierzy
Transpozycja macierzy
Obliczanie wartości własnych (ang. eigenvalues) i wektorów własnych (ang. eigenvectors)¹
Obliczanie wyznacznika macierzy

Wyznacznik (determinant) macierzy jest wartością liczbową, która jest przypisana do każdej macierzy kwadratowej. Wyznacznik macierzy jest jednym z podstawowych parametrów macierzy, który określa jej właściwości.

R
Python

mat = matrix(1:4, nrow = 2)
det(mat)

[1] -2

import numpy as np
mat = np.array([[1, 2], [3, 4]])
np.linalg.det(mat)

-2.0000000000000004

3.6 Algebra tablic

Dla tablic o takiej samej wielkości operacje algebraiczne wykonujemy w taki sam sposób jak w przypadku pojedycznych zmiennych.

\[ \begin{bmatrix} 1 & 2 & 3 & 4 \end{bmatrix} + \begin{bmatrix} 5 & 6 & 7 & 8 \end{bmatrix} = \begin{bmatrix} 6 & 8 & 10 & 12 \end{bmatrix} \]

\[ \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} + \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix} = \begin{bmatrix} 6 & 8 \\ 10 & 12 \end{bmatrix} \]

R
Python

mat1 = matrix(1:4, nrow = 1)
mat2 = matrix(5:8, nrow = 1)
mat1 + mat2

     [,1] [,2] [,3] [,4]
[1,]    6    8   10   12

mat1 = matrix(1:4, nrow = 2, byrow = TRUE)
mat2 = matrix(5:8, nrow = 2, byrow = TRUE)
mat1 + mat2

     [,1] [,2]
[1,]    6    8
[2,]   10   12

import numpy as np
mat1 = np.array([1, 2, 3, 4])
mat2 = np.array([5, 6, 7, 8])
mat1 + mat2

array([ 6,  8, 10, 12])

mat1 = np.array([[1, 2], [3, 4]])
mat2 = np.array([[5, 6], [7, 8]])
mat1 + mat2

array([[ 6,  8],
       [10, 12]])

Specyficznym przypadkiem jest mnożenie macierzy, które nie jest realizowane jako mnożenie element po elemencie, ale jako operacja matematyczna zgodnie z regułami rachunku macierzowego.

\[ \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \times \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix} = \begin{bmatrix} 1*5 + 2*7 & 1*6 + 2*8 \\ 3*5 + 4*7 & 3*6 + 4*8 \end{bmatrix} = \begin{bmatrix} 19 & 22 \\ 43 & 50 \end{bmatrix} \]

R
Python

mat1 = matrix(1:4, nrow = 2, byrow = TRUE)
mat2 = matrix(5:8, nrow = 2, byrow = TRUE)
mat1 %*% mat2

     [,1] [,2]
[1,]   19   22
[2,]   43   50

import numpy as np
mat1 = np.array([[1, 2], [3, 4]])
mat2 = np.array([[5, 6], [7, 8]])
np.dot(mat1, mat2)

array([[19, 22],
       [43, 50]])

Jeżeli tablice mają tyle samo elementów, ale mają różną wymiarowość (kształt), to działanie zależy od implementacji. Zarówno R jak i Python mają zaimplementowane operacje na tablicach o różnych wymiarach, ale w przypadku niektórych operacji, na przykład dodawania, muszą być spełnione pewne warunki. W sytuacji, gdy tablice mają różną liczbę elementów, operacja nie jest możliwa i zwracany jest błąd. Wykonanie takiej operacji wymaga przekształcenia tablic do takiej samej wymiarowości.

R
Python

mat1 = matrix(1:4, nrow = 1)
mat2 = matrix(5:8, nrow = 2, byrow = TRUE)
mat1 + mat2

Error in mat1 + mat2: non-conformable arrays

mat1 = matrix(1:4, nrow = 1)
mat2 = matrix(5:8, nrow = 2, byrow = TRUE)
mat1 = matrix(mat1, nrow = 2, byrow = TRUE)
mat1 + mat2

     [,1] [,2]
[1,]    6    8
[2,]   10   12

mat1 = np.array([1, 2, 3, 4])
mat2 = np.array([[5, 6], [7, 8]])
mat1 + mat2

operands could not be broadcast together with shapes (4,) (2,2)

mat1 = np.array([1, 2, 3, 4])
mat2 = np.array([[5, 6], [7, 8]])
mat1 = mat1.reshape(2, 2) 
mat1 + mat2

array([[ 6,  8],
       [10, 12]])

W przypadku języka R możliwe jest wykonywanie operacji pomiędzy macierzą a wektorem. Wówczas wektor jest automatycznie przekształcany do macierzy o takim samym kształcie jak drugi obiekt

3.7 Wybrane typy macierzy

Istnieje kilka specyficznych typów macierzy, które mają szczególne znaczenie w rachunku macierzowym:

Macierz jednostkowa
Macierz odwrotna
Macierz osobliwa
Macierz transponowana
Macierz symetryczna

3.7.1 Macierz jednostkowa

Macierz jednostkowa (ang. identity) to szczególny przypadek macierzy, gdzie wszystkie elementy leżące na przekątnej wynoszą 1 a pozostałe elementy w obu połówkach macierzy wynoszą 0.

\[ A = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \]

Wyznacznik macierzy jednostkowej wynosi 1.

\[ \det(A) = 1 \]

R
Python

mat_jedn = diag(4)
mat_jedn

     [,1] [,2] [,3] [,4]
[1,]    1    0    0    0
[2,]    0    1    0    0
[3,]    0    0    1    0
[4,]    0    0    0    1

det(mat_jedn)

[1] 1

import numpy as np
mat_jedn = np.eye(4)
mat_jedn

array([[1., 0., 0., 0.],
       [0., 1., 0., 0.],
       [0., 0., 1., 0.],
       [0., 0., 0., 1.]])

np.linalg.det(mat_jedn)

1.0

Macierz jednostkowa jest elementem obustronnie nautralnym w procesie mnożenia macierzy, podobnie jak 1 w przypadku wartości skalarnych. Inaczej mówiąc, pomnożenie macierzy przez macierz jednostkową daje tą samą macierz.

R
Python

mat = matrix(1:16, nrow = 4)
mat %*% mat_jedn

     [,1] [,2] [,3] [,4]
[1,]    1    5    9   13
[2,]    2    6   10   14
[3,]    3    7   11   15
[4,]    4    8   12   16

mat = np.array(range(1, 17)).reshape(4, 4)
np.dot(mat, mat_jedn)

array([[ 1.,  2.,  3.,  4.],
       [ 5.,  6.,  7.,  8.],
       [ 9., 10., 11., 12.],
       [13., 14., 15., 16.]])

Macierze, których wartości przekątnej są równe pewnej stałej wartości, a pozostałe wartości są równe 0, nazywa się macierzą skalarną. Macierz taka powstaje w wyniku przemnożenia macierzy jednostkowej przez pewną stałą wartość, zwaną skalarem.

Macierze jednostkowe są stosowane w wielu algorytmach numerycznych, na przykład do rozwiązywania układów równań liniowych. Macierz jednostkowa jest również używana do przekształcania macierzy, na przykład w przypadku obliczania macierzy odwrotnej.

3.7.2 Macierz odwrotna

Macierz odwrotna (ang, inverse) \(A^{-1}\) do macierzy \(A\), to taka macierz, która spełnia następujący warunek \(A * A^{-1} = A^{-1} * A = I\), gdzie \(I\) to macierz jednostkowa.

\[ A = \begin{bmatrix} 1 & 1 \\ 2 & 4 \\ \end{bmatrix} ,\ A^{-1} = \begin{bmatrix} 2 & -0.5 \\ -1 & 0.5 \\ \end{bmatrix} ,\ A \times A^{-1} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} \]

R
Python

mat = matrix(c(1, 1, 2, 4), nrow = 2)
mat

     [,1] [,2]
[1,]    1    2
[2,]    1    4

mat_odw = solve(mat)
mat_odw

     [,1] [,2]
[1,]  2.0 -1.0
[2,] -0.5  0.5

mat %*% mat_odw

     [,1] [,2]
[1,]    1    0
[2,]    0    1

import numpy as np
mat = np.array([[1, 1], [2, 4]])
mat

array([[1, 1],
       [2, 4]])

mat_odw = np.linalg.inv(mat)
mat_odw

array([[ 2. , -0.5],
       [-1. ,  0.5]])

np.dot(mat, mat_odw)

array([[1., 0.],
       [0., 1.]])

Macierze odwrotne są używane do rozwiązywania układów równań liniowych², do przekształcania macierzy, itp.

R
Python

A = matrix(c(4, 3, 2, 1), nrow = 2, byrow = TRUE)
b = c(1, 2)
A_inv = solve(A)
x = A_inv %*% b
x

     [,1]
[1,]  2.5
[2,] -3.0

A = np.array([[4, 3], [2, 1]])
b = np.array([1, 2])
A_inv = np.linalg.inv(A)
x = np.dot(A_inv, b)
x

array([ 2.5, -3. ])

Macierzy odwrotnej nie należy mylić z macierzą transponowaną.

3.7.3 Macierz osobliwa

Macierz osobliwa to taka macierz, której wyznacznik jest równy 0. Jeżli jest nierówny 0, macierz nazywamy nieosobliwą. Macierz osobliwa nie ma macierzy odwrotnej.

Przykłady macierzy osobliwych:

\[ A = \begin{bmatrix} 1 & 1 \\ 0 & 0 \\ \end{bmatrix}, B = \begin{bmatrix} 1 & 1 \\ 1 & 1 \\ \end{bmatrix}, C = \begin{bmatrix} 0 & 0 \\ 0 & 0 \\ \end{bmatrix}, D = \begin{bmatrix} 0 & 0 \\ 0 & 1 \\ \end{bmatrix} \]

\[ \det(A) = 0, \det(B) = 0, \det(C) = 0, \det(D) = 0 \]

R
Python

mat = matrix(c(1, 1, 0, 0), nrow = 2)
det(mat)

[1] 0

import numpy as np
mat = np.array([[1, 1], [0, 0]])
np.linalg.det(mat)

0.0

W przypadku analizy danych macierz osobliwa często wskazuje, że dane są kolinearne, czyli że dwie lub więcej kolumn lub wierszy mają takie same wartości. Niektóre algorytmy nie mogą działać w takim przypadku i kończą działanie wyświetlając komunikat (np. system is exactly singular, Singular matrix, itp.). W praktyce oznacza, że nie można odwrócić takiej macierzy i tym samym rozwiązać układu równań, a dokładnie, nie można znaleść unikalnego rozwiązania.

R
Python

solve(mat)

Error in solve.default(mat): Lapack routine dgesv: system is exactly singular: U[2,2] = 0

np.linalg.inv(mat)

Singular matrix

W takiej sytuacji można:

usunąć nadmiarowe kolumny lub wiersze (np. zduplikowane)
dokonać drobych zmian w wartościach, na przykład poprzez dodanie nic nie znaczących wartości losowych
dokonać redukcji wymiarowości przy pomocy bardziej złożonych metod

3.7.4 Macierz transponowana

Macierz transponowana, to macierz, w której wiersze zostają zamienione kolumnami.

\[ A = \begin{bmatrix} 1 & 2 & 3 & 4\\ 3 & 2 & 1 & 5\\ 4 & 6 & 1 & 3\\ 2 & 2 & 4 & 2\\ \end{bmatrix} ,\ A^{T} = \begin{bmatrix} 1 & 3 & 4 & 2\\ 2 & 2 & 6 & 2\\ 3 & 1 & 1 & 4\\ 4 & 5 & 3 & 2\\ \end{bmatrix} \]

R
Python

mat = matrix(c(1, 3, 4, 2, 2, 2, 6, 2, 3, 1, 1, 4, 4, 5, 3, 2), nrow = 4)
mat

     [,1] [,2] [,3] [,4]
[1,]    1    2    3    4
[2,]    3    2    1    5
[3,]    4    6    1    3
[4,]    2    2    4    2

mat_t = t(mat)
mat_t

     [,1] [,2] [,3] [,4]
[1,]    1    3    4    2
[2,]    2    2    6    2
[3,]    3    1    1    4
[4,]    4    5    3    2

import numpy as np
mat = np.array([[1, 2, 3, 4], [3, 2, 1, 5], [4, 6, 1, 3], [2, 2, 4, 2]])
mat

array([[1, 2, 3, 4],
       [3, 2, 1, 5],
       [4, 6, 1, 3],
       [2, 2, 4, 2]])

mat_t = mat.T
mat_t

array([[1, 3, 4, 2],
       [2, 2, 6, 2],
       [3, 1, 1, 4],
       [4, 5, 3, 2]])

Proces transpozycji macierzy jest jedną z ważniejszych funkcjonalności oprogramowania numerycznego. Sposób uprządkowania danych (wierszach lub w kolumnach) ma znaczenie przy wielu algorytmach obliczeniowych. Na przykład standardowo, dane w macierzch indeksowane są najpierw w wierszch, a następnie w kolumnach.

R
Python

gm = readr::read_csv("data/gapminder_1950_2023.csv")
gm2000 = subset(gm, Rok == 2000)
cor_mat = cor(gm2000[, 4:8], use = "pairwise.complete.obs")
cor_mat_t = t(cor_mat)
avg_cor = rowMeans(cor_mat_t)
avg_cor

   Populacja PKB_na_osobe Ocz_dl_zycia CO2_na_osobe     Plodnosc 
   0.1589629    0.3514573    0.2446784    0.3481406   -0.1682657

import pandas as pd
import numpy as np
gm = pd.read_csv("data/gapminder_1950_2023.csv")
gm2000 = gm[gm["Rok"] == 2000]
cor_mat = gm2000.iloc[:, 3:8].corr()
cor_mat_t = cor_mat.T
avg_cor = cor_mat_t.mean()
avg_cor

Populacja       0.158963
PKB_na_osobe    0.351457
Ocz_dl_zycia    0.244678
CO2_na_osobe    0.348141
Plodnosc       -0.168266
dtype: float64

3.7.5 Macierz symetryczna

Macierz symetryczna to taka, która posiada symetrię poprzez główną przekątną. Zawartość przekątnej może być dowolna.

\[ A = \begin{bmatrix} 1 & 2 & 3 & 4\\ 2 & 5 & 3 & 4\\ 3 & 3 & 6 & 4\\ 4 & 4 & 4 & 7\\ \end{bmatrix} ,\ B = \begin{bmatrix} 1 & 2 & 3 & 4\\ 2 & 1 & 3 & 4\\ 3 & 3 & 1 & 4\\ 4 & 4 & 4 & 1\\ \end{bmatrix} \]

Właściwością macierzy symetrycznej jest to, że w wyniku transpozycji otrzymujemy kopię macierzy: \(A = A^{T}\).

R
Python

mat = matrix(c(1, 2, 3, 4, 2, 5, 3, 4, 3, 3, 6, 4, 4, 4, 4, 7), nrow = 4)
mat

     [,1] [,2] [,3] [,4]
[1,]    1    2    3    4
[2,]    2    5    3    4
[3,]    3    3    6    4
[4,]    4    4    4    7

mat_t = t(mat)
mat_t

     [,1] [,2] [,3] [,4]
[1,]    1    2    3    4
[2,]    2    5    3    4
[3,]    3    3    6    4
[4,]    4    4    4    7

identical(mat, mat_t)

[1] TRUE

import numpy as np
mat = np.array([[1, 2, 3, 4], [2, 5, 3, 4], [3, 3, 6, 4], [4, 4, 4, 7]])
mat

array([[1, 2, 3, 4],
       [2, 5, 3, 4],
       [3, 3, 6, 4],
       [4, 4, 4, 7]])

mat_t = mat.T
mat_t

array([[1, 2, 3, 4],
       [2, 5, 3, 4],
       [3, 3, 6, 4],
       [4, 4, 4, 7]])

np.array_equal(mat, mat_t)

True

Macierze symetryczne mają zastsowanie do wyrażania relacji pomiędzy wszystkimi obiektami w zbiorze jako macierze podobieństwa, odległości, korelacji, itp. W zbiorze zawierającym m cech (kolumn) i n przypadków (wierszy), macierz odległości i podobieństwa dotyczy raczej przypadków/obiektów i ma wymiar \(n \times n\), natomiast macierz korelacji dotyczy cech/atrybutów i ma wymiar \(m \times m\).

Macierz symetryczna może być przedstawiona w postaci połówki macierzy i jej przekątnej jeżeli ta jest niezerowa. Macierze symetryczne służą do opisu zjawisk symetrycznych, na przykład macierz odległości w przestrzeni geograficznej między punktami, jeżeli nie podlegają one innym ograniczeniom będzie macierzą symetryczną. Macierze wykresów ilustrujące zależności pomiędzy cechami opisującymi jakieś zjawisko są macierzami symetrycznymi, co oznacza, że można stosować różne formy prezentacji zależności dla obu połówek, a przekątną wykorzystać do ilustracji rozkładu cech zmiennych.

R
Python

library(ggplot2)
library(GGally)
gm = readr::read_csv("data/gapminder_1950_2023.csv")
gm2000 = subset(gm, Rok == 2000)
ggpairs(gm2000[, 4:8])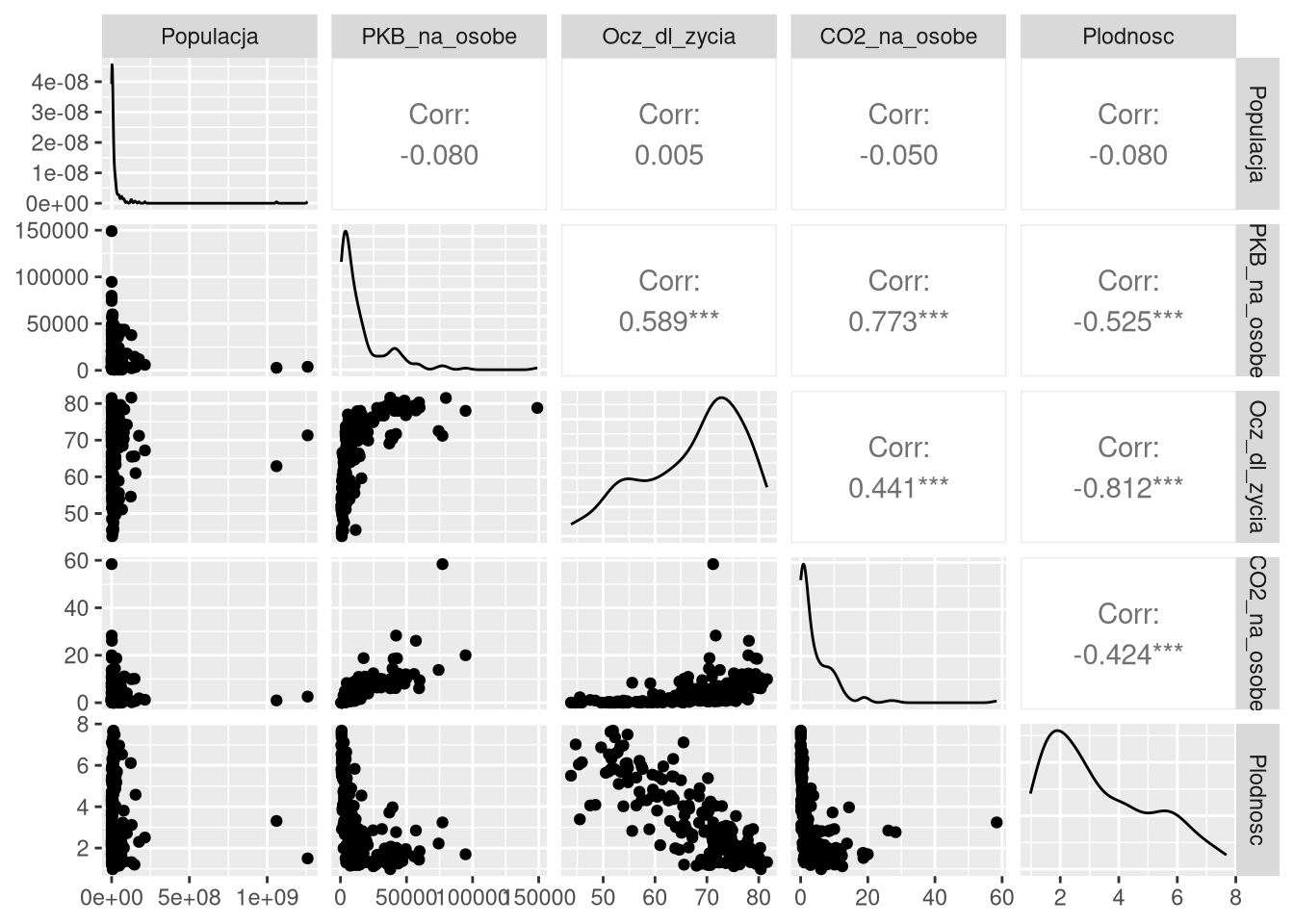

import pandas as pd
import seaborn as sns
gm = pd.read_csv("data/gapminder_1950_2023.csv")
gm2000 = gm[gm["Rok"] == 2000]
sns.pairplot(gm2000.iloc[:, 3:8])

W przypadku przetwarzania macierzy możemy pozyskać/zmienić dane osobno w każdej połówce macierzy oraz na jej przekątnej.

Wartości własne i wektory własne są parametrami macierzy, które określają jej właściwości. Są one wykorzystywane, między innymi, do analizy głównych składowych (ang. principal component analysis, PCA), w algorytmach 6grafowych, czy przetwarzaniu sygnałów.↩︎
Np. rozwiązanie x układu Ax = b to x = A^-1 * b↩︎