5  Metody graficznej prezentacji danych

5.1 Gramatyka grafiki

Gramatyka: zbiór reguł opisujących system języka (Słownik PWN)

Gramatyka grafiki to podejście opisywania i konstruowania wizualizacji lub grafik w ustrukturyzowany sposób. Cechy gramatyki grafiki obejmują jej systematyzację i formalizację, logiczny rozkład wykresu na części składowe, a także uniwersalność, czyli niezależność od konkretnego narzędzia czy implementacji. Idee gramatyki grafiki zostały zaproponowane przez Lelanda Wilkinsona w książce The Grammar of Graphics (Wilkinson (2005)), budując na wcześniejszych pracach, między innymi, Jacques’a Bertina (Bertin (1983)).

Wilkinson zaproponował sześć podstawowych elementów gramatyki grafiki:

1. DATA: zbiór operacji wyodrębniającej zmienne z danych
2. TRANS: transformacje zmiennych
3. SCALE: transformacje skali
4. COORD: wybór układu odniesienia
5. ELEMENT: geometria i estetyka
6. GUIDE: elementy wykresu

Idee Wilkinsona zostały rozpowszechnione oraz zaimplementowane (z pewnymi zmianami) w języku programowania R w pakiecie ggplot2 (Wickham (2010)). Zainspirowało to powstanie innych narzędzi opartych na gramatyce grafiki, np. plotly, Altair, vega, czy plotnine.

Bez względu na implementację, konieczne jest przetłumaczenie opisu wykresu wykonanego w ramach języka programowania na język opisu geometrii, która zostanie użyta do narysowania wykresu na urządzeniu (np. PDF). Gramatyka grafiki odpowiada za tłumaczenie języka opisu danych na język opisu obiektów graficznych.

5.2 Przestrzeń wykresu

Przestrzeń wykresu to obszar, na którym rysowany jest wykres. Konkretne miejsce na wykresie można określić za pomocą:

1. Pikseli
2. Przestrzeni danych
3. Przestrzeni znormalizowanej (0, 1)

Wszystkie te przestrzenie można przeliczać na siebie, np. przestrzeń danych na piksele, czy przestrzeń znormalizowaną na przestrzeń danych.

5.3 Przykład grafiki

1. Dane wejściowe, czyli zbiór obserwacji dla szeregu zmiennych, które chcemy przedstawić na wykresie. W poniższym przykładzie mamy cztery obserwacje dla zmiennych A, B, C, D.

dfs1 = data.frame(A = c(2, 1, 4, 9), B = c(3, 2, 5, 10), 
                  C = c(4, 1, 15, 80), D = c("a", "a", "b", "b"))
dfs1

  A  B  C D
1 2  3  4 a
2 1  2  1 a
3 4  5 15 b
4 9 10 80 b

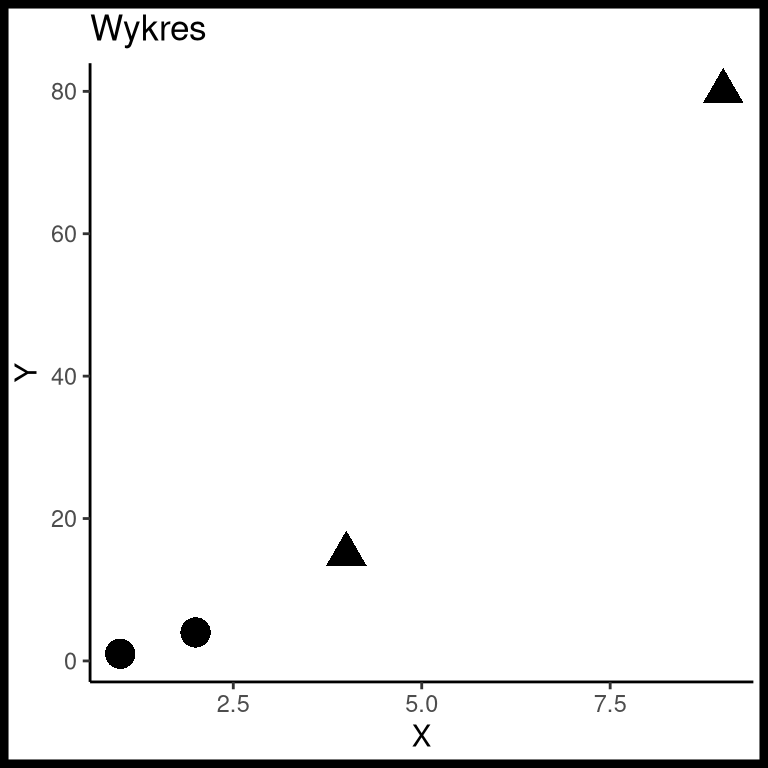
2. W kolejnym kroku wybieramy zmienne, które chcemy przedstawić na wykresie, a następnie określamy dla nich rodzaj zmiennych wizualnych. Tutaj wybraliśmy zmienne X i Y, które chcemy przedstawić na wykresie punktowym, gdzie kształt punktów zależy od zmiennej Shape.

dfs2 = data.frame(X = c(2, 1, 4, 9),
                  Y = c(4, 1, 15, 80),
                  Shape = c("a", "a", "b", "b"))
dfs2

  X  Y Shape
1 2  4     a
2 1  1     a
3 4 15     b
4 9 80     b

3. Następy krok to przypisanie wybranych zmiennych do zmiennych wizualnych, czyli określenie, jak mają być przedstawione na wykresie.

dfs3 = data.frame(x = c(25, 0, 75, 200),
                  y = c(11, 0, 53, 300),
                  shape = c("circle", "circle", "square", "square"))
dfs3

    x   y  shape
1  25  11 circle
2   0   0 circle
3  75  53 square
4 200 300 square

4. Wybrane zmienne wizualne są przypisywane do konkretnej lokalizacji na wykresie, czyli do konkretnych pikseli, przestrzeni danych, czy przestrzeni znormalizowanej. Dalej są one łączone z osiami wykresu i jego przestrzenią.

5. Ostatni krok to wygenerowanie wykresu.

5.4 Implementacja gramatyki grafiki w ggplot2

Jak wspomniano wcześniej, ggplot2 to implementacja gramatyki grafiki w języku programowania R. Ta implementacja opiera się też na pewnych zmianach względem oryginalnej koncepcji Wilkinsona i często określana jest jako warstwowa gramatyka grafiki (ang. layered grammar of graphics).

Rysunek 5.1: Relacja między gramatyką grafiki a implementacją ggplot2. Źródło: Wickham (2010)

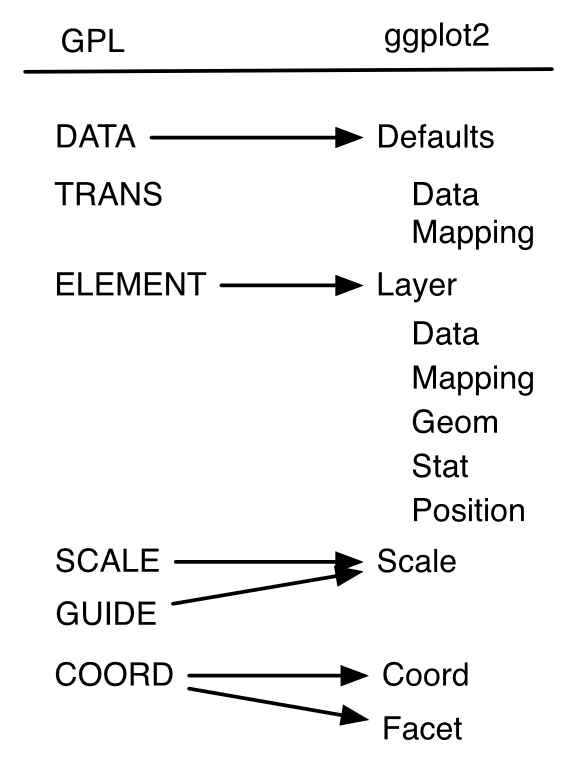
TRANS (transformacje zmiennych) nie są elementem gramatyki grafiki w ggplot2, ponieważ można je wykonać w R, np. przed wywołaniem funkcji ggplot(). Przykładowe operacje to zamiana zmiennej na typ czynnikowy, czy posortowanie danych.

Rysunek 5.2: Zależności między elementami gramatyki grafiki w ggplot2. Źródło: Biecek (2016)

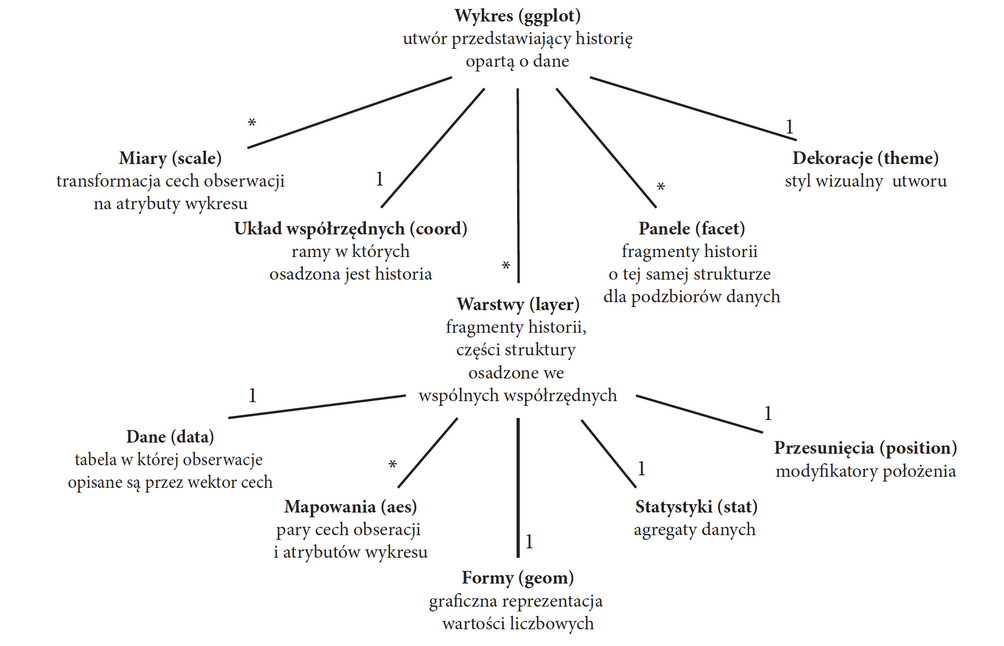
library(ggplot2)

5.4.1 Dane (data)

Jakie dane chcemy użyć?

Dane do wykresu należy wczytać do R, a następnie przekształcić do odpowiedniej postaci (Sekcja 1.2.1).

Dane wersja 1:

df3

# A tibble: 14,060 × 3
   ID             Ocz_dl_zycia PKB_na_osobe
   <chr>                 <dbl>        <dbl>
 1 Australia_1950         69.4        16400
 2 Australia_1951         69.2        16500
 3 Australia_1952         69.5        16200
 4 Australia_1953         69.9        16500
 5 Australia_1954         70.2        17100
 6 Australia_1955         70.3        17600
 7 Australia_1956         70.4        17600
 8 Australia_1957         70.6        17500
 9 Australia_1958         71          18000
10 Australia_1959         70.9        18600
# ℹ 14,050 more rows

Dane wersja 2:

df1

# A tibble: 14,060 × 4
   Kraj        Rok Ocz_dl_zycia PKB_na_osobe
   <chr>     <dbl>        <dbl>        <dbl>
 1 Australia  1950         69.4        16400
 2 Australia  1951         69.2        16500
 3 Australia  1952         69.5        16200
 4 Australia  1953         69.9        16500
 5 Australia  1954         70.2        17100
 6 Australia  1955         70.3        17600
 7 Australia  1956         70.4        17600
 8 Australia  1957         70.6        17500
 9 Australia  1958         71          18000
10 Australia  1959         70.9        18600
# ℹ 14,050 more rows

Dane wersja 3:

df2

# A tibble: 28,120 × 4
   Kraj        Rok Zmienna      Wartosc
   <chr>     <dbl> <chr>          <dbl>
 1 Australia  1950 Ocz_dl_zycia    69.4
 2 Australia  1950 PKB_na_osobe 16400  
 3 Australia  1951 Ocz_dl_zycia    69.2
 4 Australia  1951 PKB_na_osobe 16500  
 5 Australia  1952 Ocz_dl_zycia    69.5
 6 Australia  1952 PKB_na_osobe 16200  
 7 Australia  1953 Ocz_dl_zycia    69.9
 8 Australia  1953 PKB_na_osobe 16500  
 9 Australia  1954 Ocz_dl_zycia    70.2
10 Australia  1954 PKB_na_osobe 17100  
# ℹ 28,110 more rows

5.4.2 DATA a ELEMENT

Defaults a layer

library(ggplot2)
ggplot(df0sel, aes(Region, Ocz_dl_zycia, color = Region)) + 
    geom_violin() +
    geom_jitter()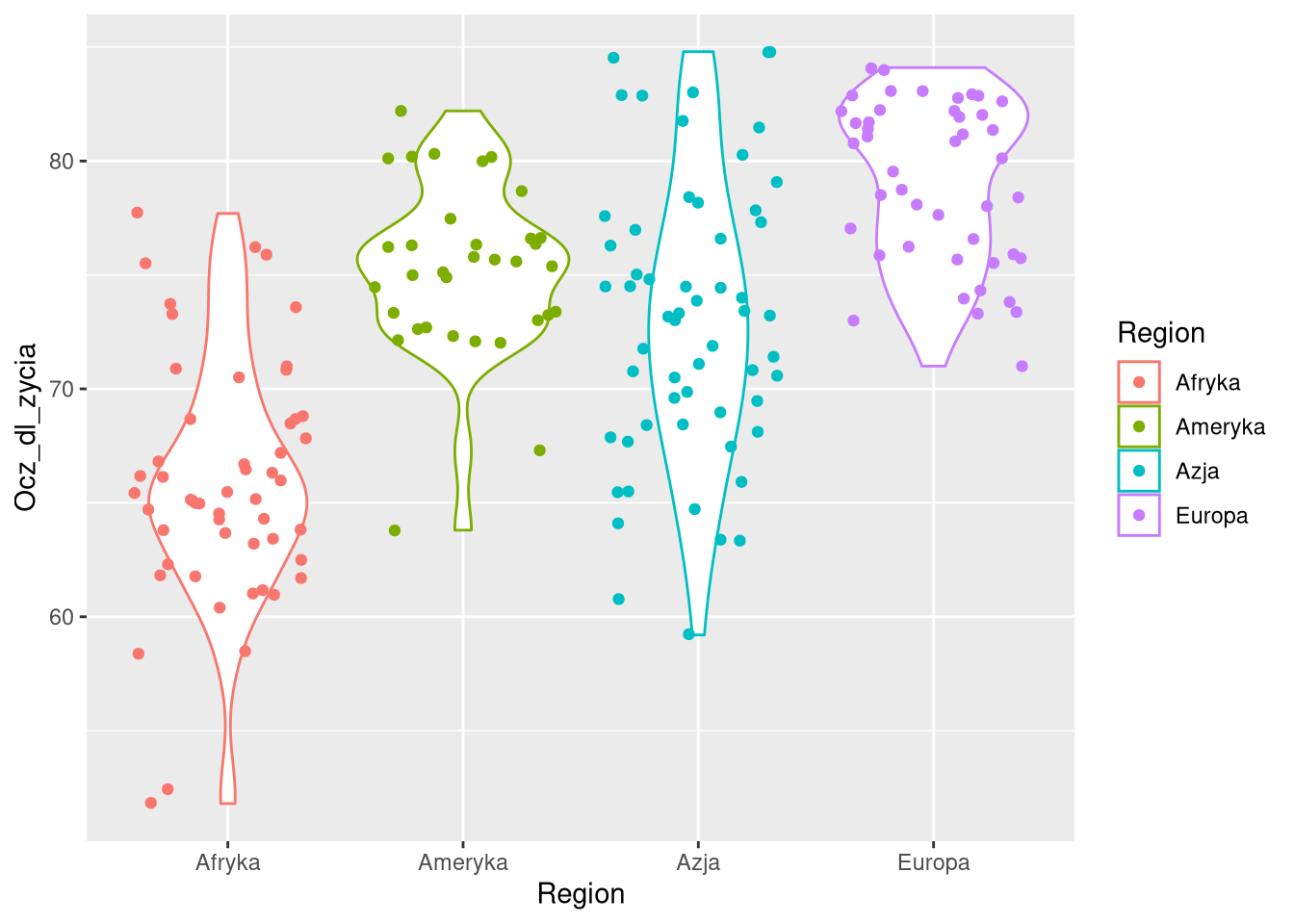

ggplot(df0sel, aes(Region, Ocz_dl_zycia)) + 
    geom_violin() +
    geom_jitter(aes(color = Region))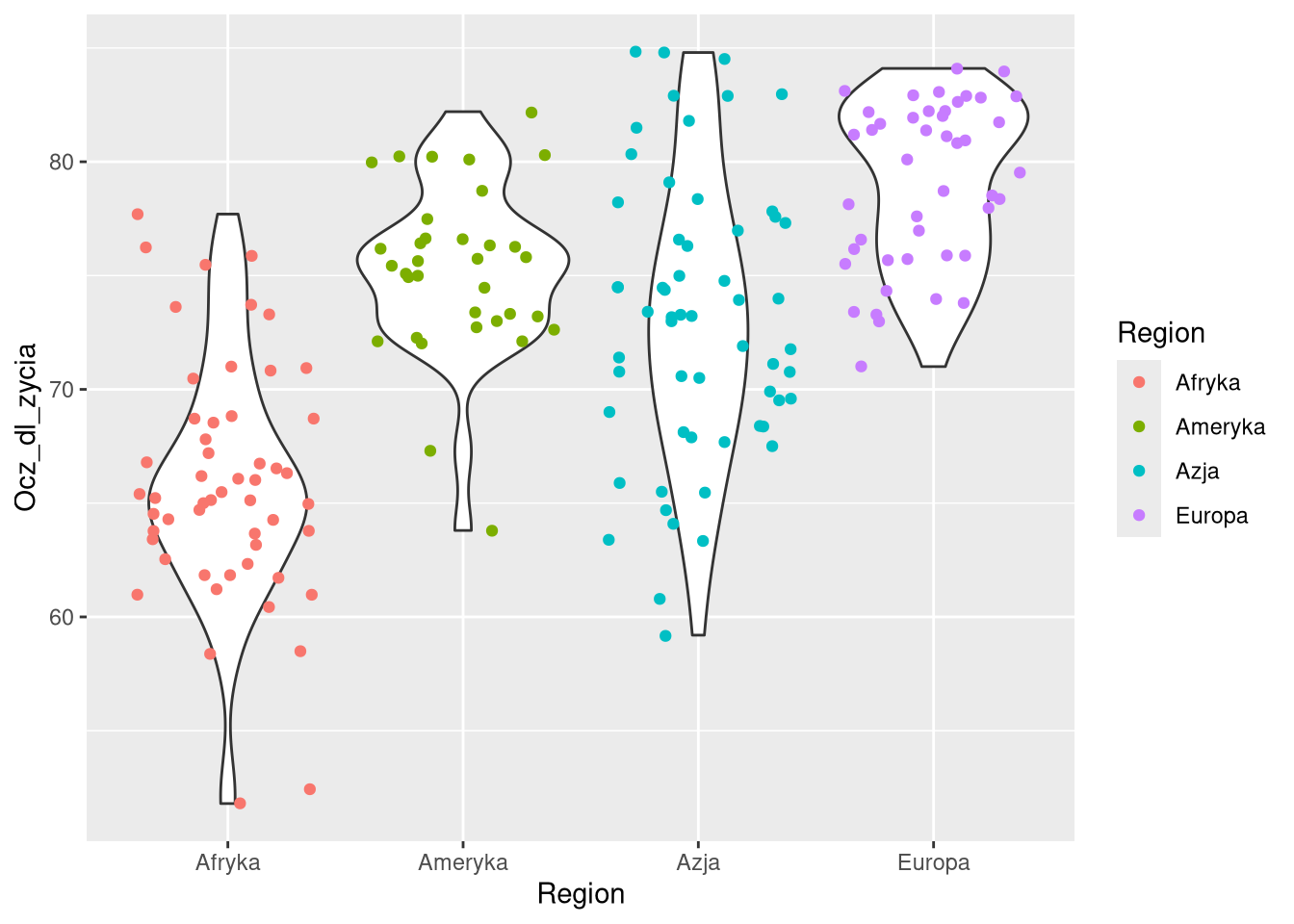

ggplot(df0sel, aes(Region, Ocz_dl_zycia)) + 
    geom_violin(aes(fill = Region)) +
    geom_jitter()

5.4.3 Warstwa

5.4.3.1 Mapowanie

Jakie zmienne chcemy pokazać?

Mapowanie to przypisanie zmiennych do zmiennych wizualnych, takich jak pozycja, kształt, kolor, wielkość, itd.

df1pol = filter(df1, Kraj == "Polska")
ggplot(df1pol, aes(Rok, PKB_na_osobe))

ggplot(df1pol, aes(Rok, PKB_na_osobe)) + 
    geom_line()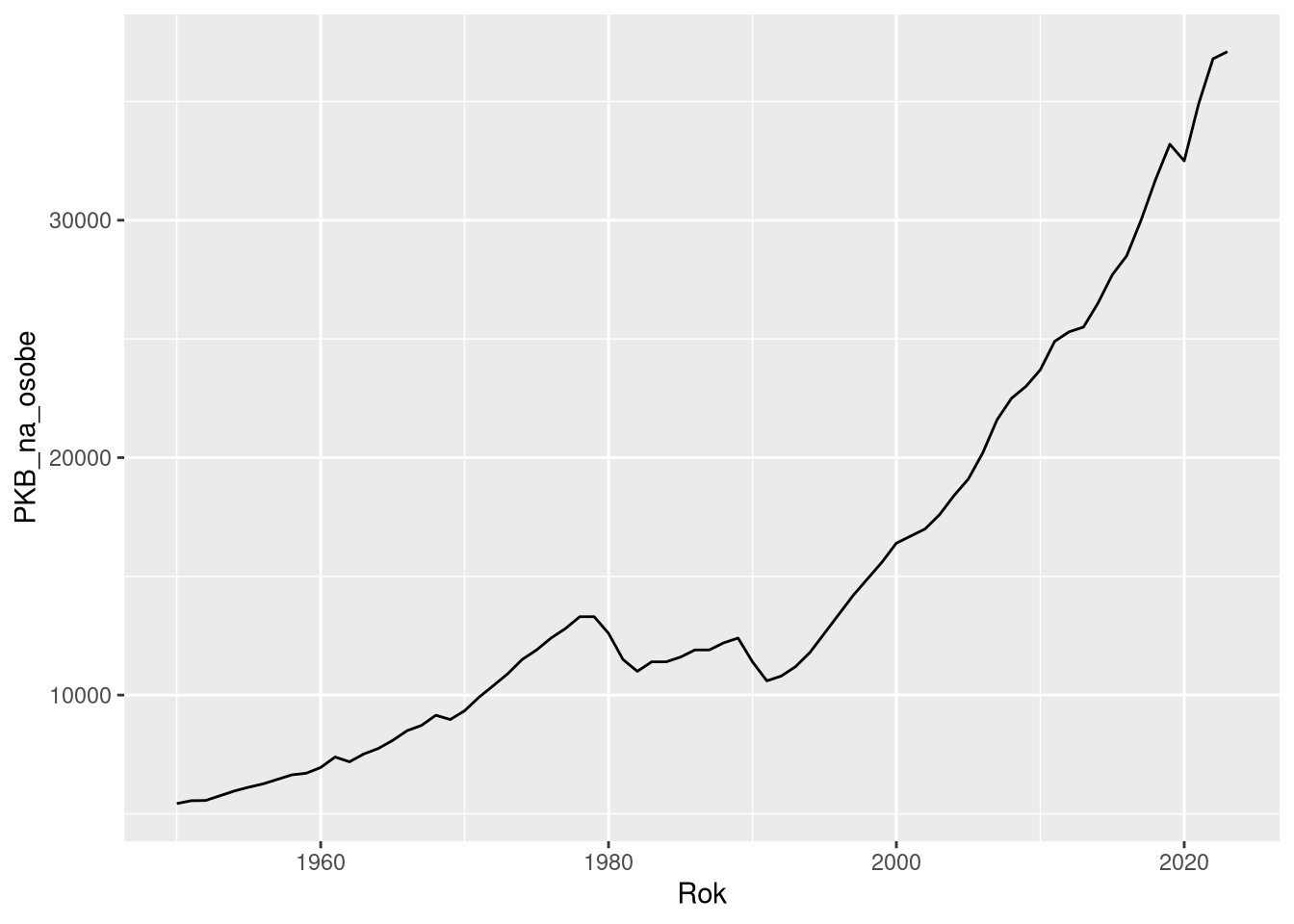

df2pol = filter(df2, Kraj == "Polska")
ggplot(df2pol, aes(Rok, Wartosc, color = Zmienna)) +
    geom_line()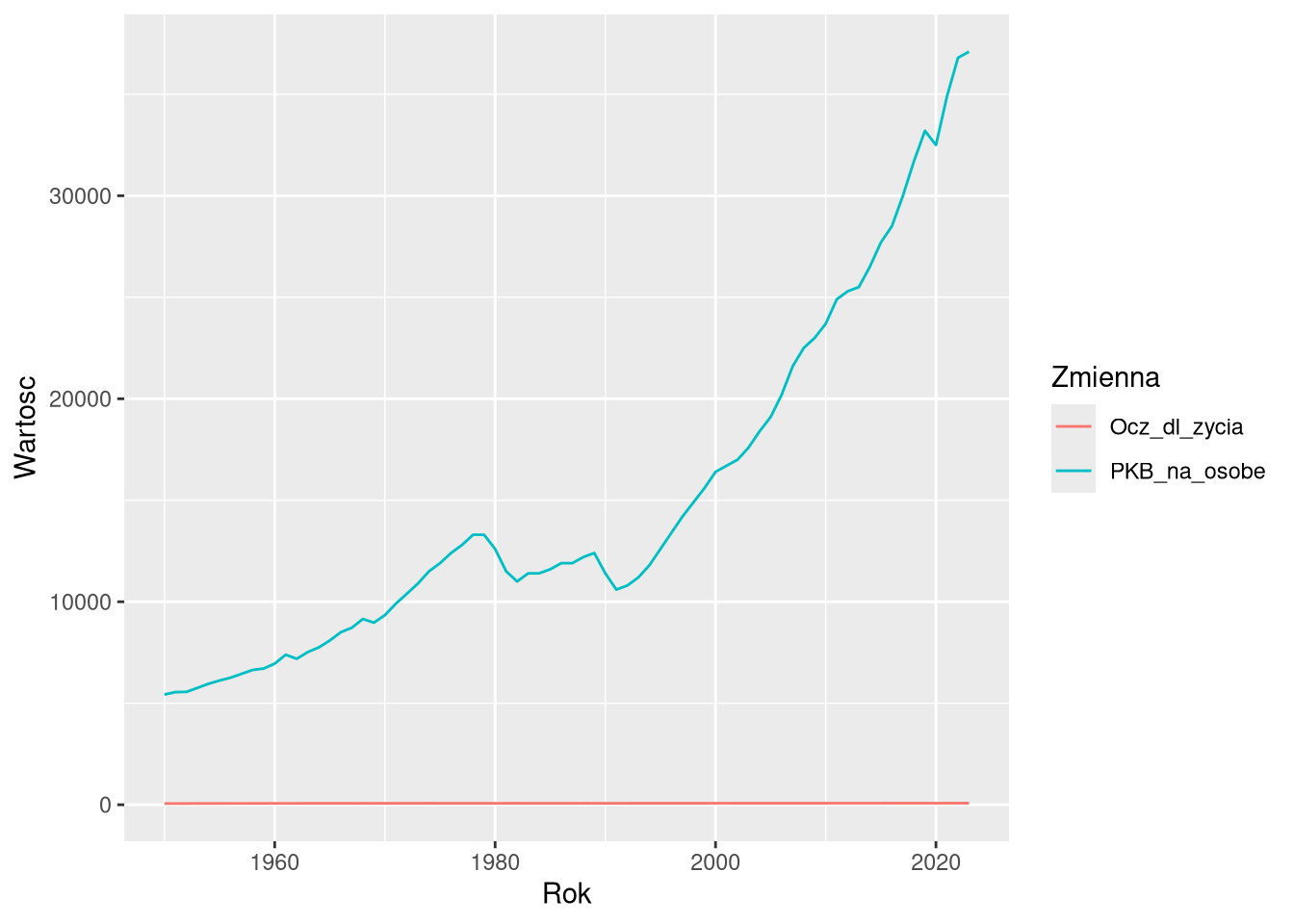

df0 = filter(gm0, Rok %in% c(1900, 1950, 2000))
ggplot(df0, aes(Plodnosc, Ocz_dl_zycia, 
                color = as.factor(Rok), shape = Region, size = PKB_na_osobe)) +
    geom_point()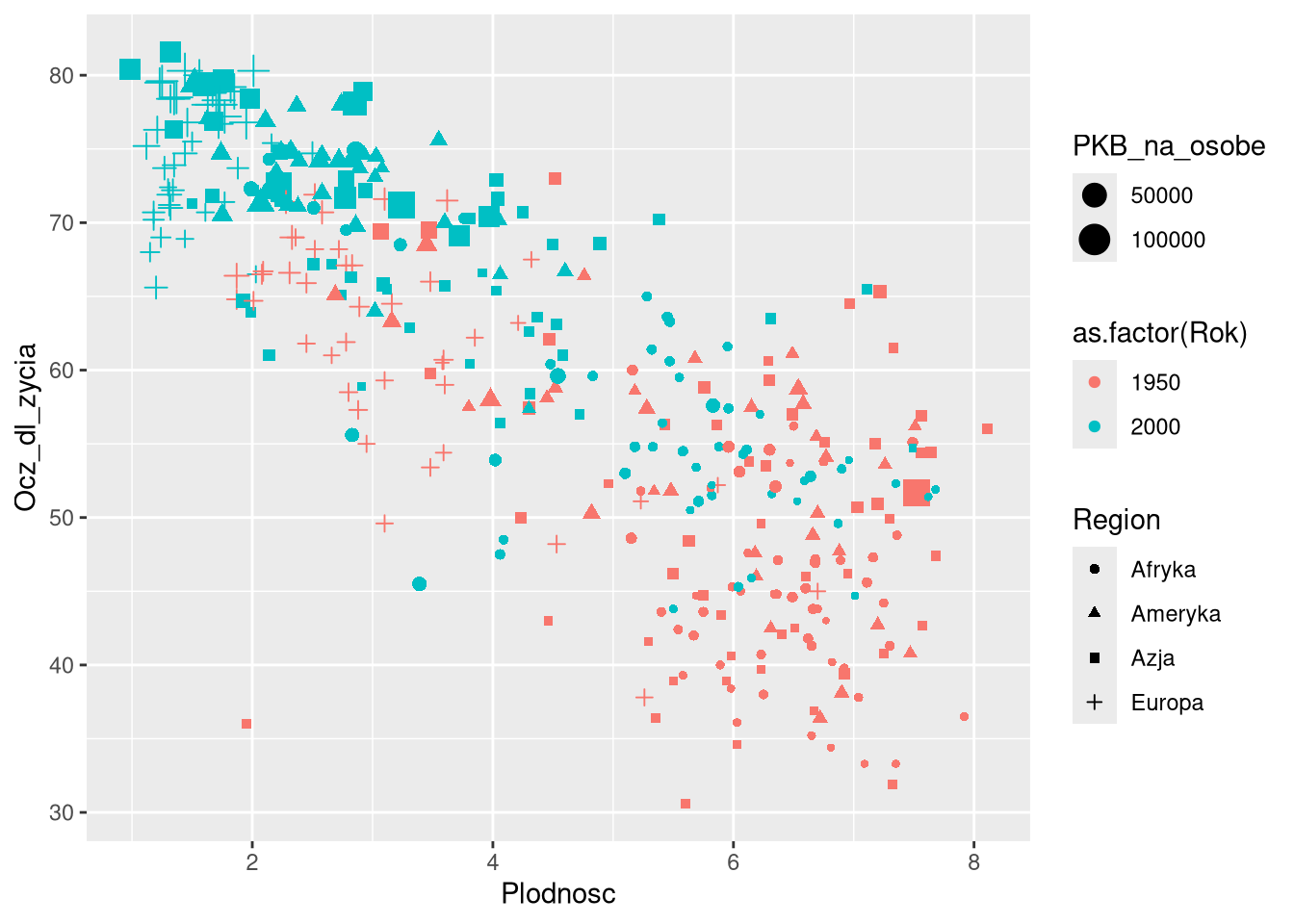

5.4.3.2 Formy

Jaki rodzaj form (geometrii) chcemy użyć?

Formy (ang. geoms) to elementy wykresu, np. punkty, linie, prostokąty, tekst, ścieżki, poligony, histogramy, wykresy pudełkowe, wykresy skrzypcowe, wykresy zawierające zakresy błędu/niepewności, itd.

Formy mogą mieć różne wymiary:

• 0 wymiarów: punkt, tekst
• 1 wymiar: linia, ścieżka
• 2 wymiary: poligon, zakres

Punkty (kropki) pozwalają na pokazanie wartości dwóch, często niezależnych, zmiennych. Ich relacja pozwala na wnioskowanie o zależnościach między zmiennymi. Taka forma pozwala na umieszczenie wielu obserwacji na wykresie, do których można dalej przypisać kolejne atrybuty używając zmiennych wizualnych (wielkość, kształt, kolor, itd.). Są one także dobrym uzupełnieniem innych warstw na wykresie. Punkty mają też swoje ograniczenia. Mała liczba przedstawianych punktów pozostawia dużo pustego miejsca na wykresie, a duża liczba punktów może na siebie nachodzić, co utrudnia odczytanie wykresu.

ggplot(df1pol, aes(Rok, PKB_na_osobe)) + geom_point(size = 0.1)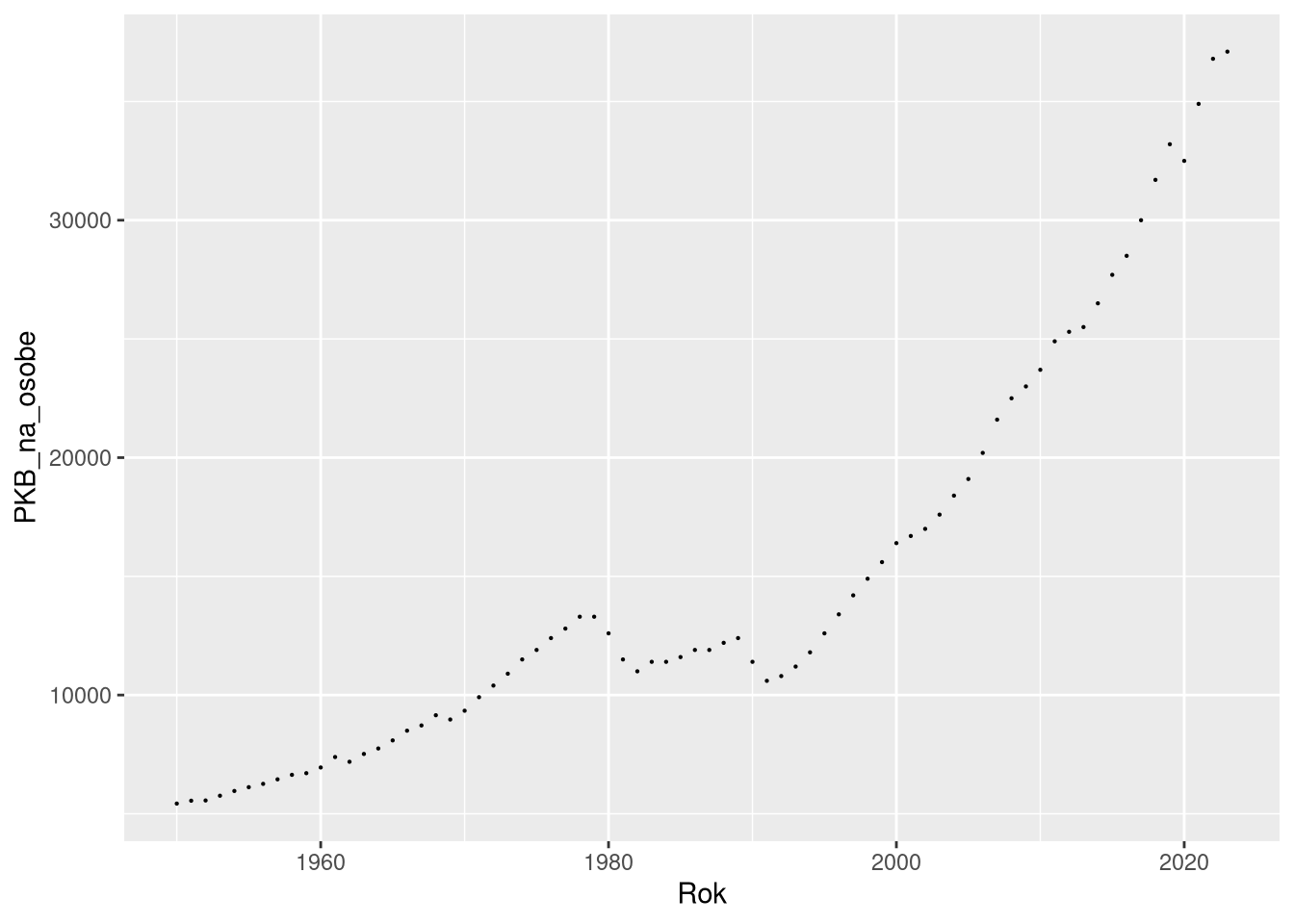

Linie nadają się do pokazywania zmian w czasie, czy też wizualizacji par lub zbiorów zależnych obserwacji. W takiej sytuacji linie łączą punkty odpowiadające tym parom, a wiele par może być przypisanych do jedej linii: inaczej mówiąc każda linia może być traktowana jak grupa punktów. Linie moją być reprezentowane przez kolory, szerokość, typ linii, itd. Z uwagi na to, że linie są ciągłe, często stosowane są do przedstaiwania trendów czy zmian w czasie. Z drugiej strony, w przypadku braku jednoznacznego trendu, wiele linii może się przecinać, co utrudnia odczytanie wykresu.

ggplot(df1pol, aes(Rok, PKB_na_osobe)) + geom_line()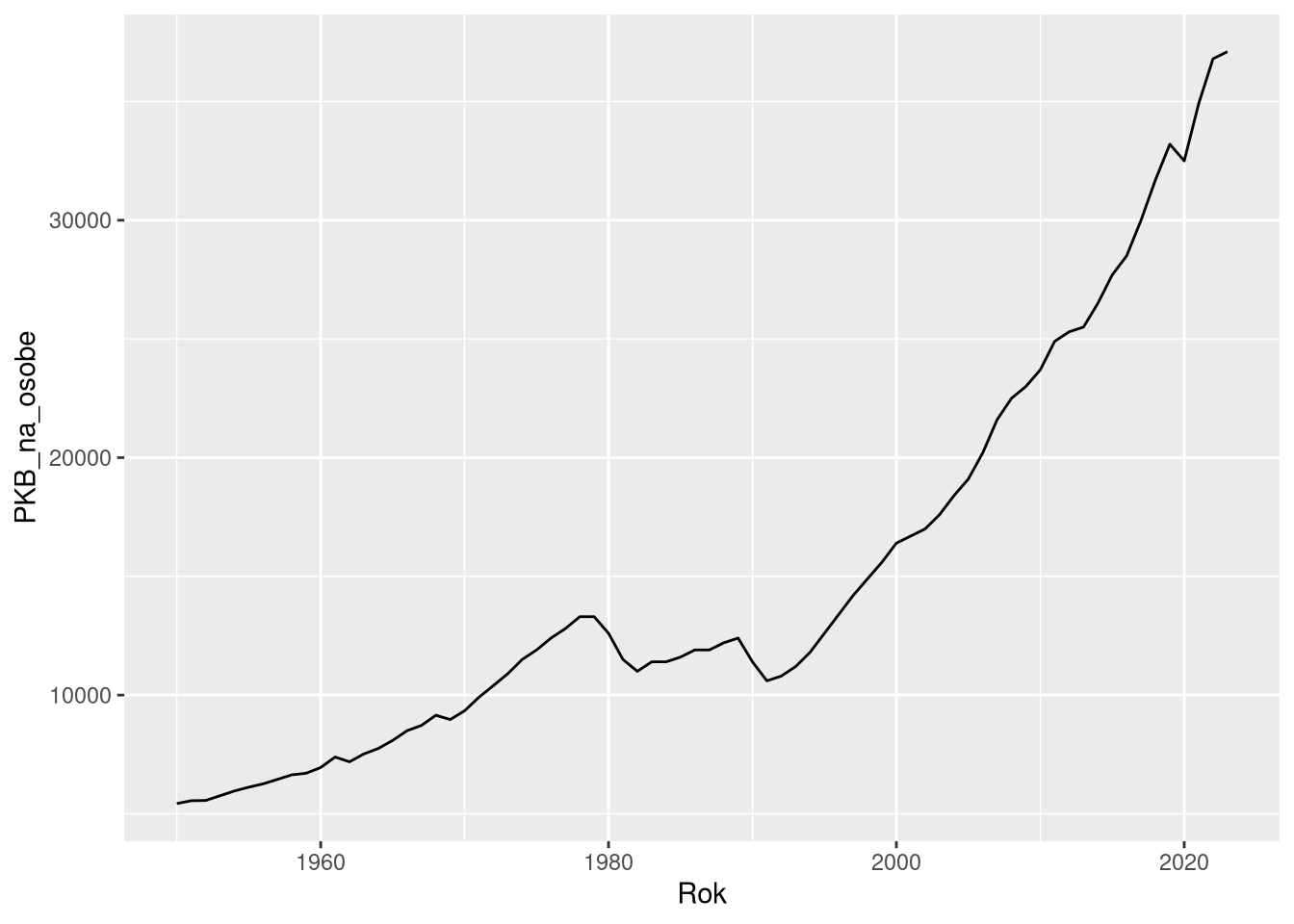

Poligony (powierzchnie) są często używane w wykresach w postaci prostokątów. Wiele prostokątów ułożonych obok siebie tworzy wykresy słupkowy czy histogram. Najczęściej długość takich prostokątów powiązana jest z wartościami zmiennej, a ich szerokość jest stała. Od tego schematu mogą być różne odstępstwa, np. wykresy mozaikowe czy treemap, gdzie szerokość prostokątów lub ich powierzchnia jest proporcjonalna do wartości zmiennej. Poligony mogą być także nieregularne, pokazując, np. zmianę wielkości danej zmiennej. Poligony pokazują informację za pomocą swojego położenia czy wielkości (długości lub powierzchni), ale także używając koloru, tekstury, czy też koloru krawędzi. Prostokąty pozwalaja na łatwe porównanie długości, szczególnie w przypadku ich ułożenia obok siebie. Z drugiej strony, porównanie pól poligonów jest znacznie trudniejsze, w szczególności gdy mają one nieregularny kształt.

ggplot(df1pol, aes(Rok, PKB_na_osobe)) + geom_area()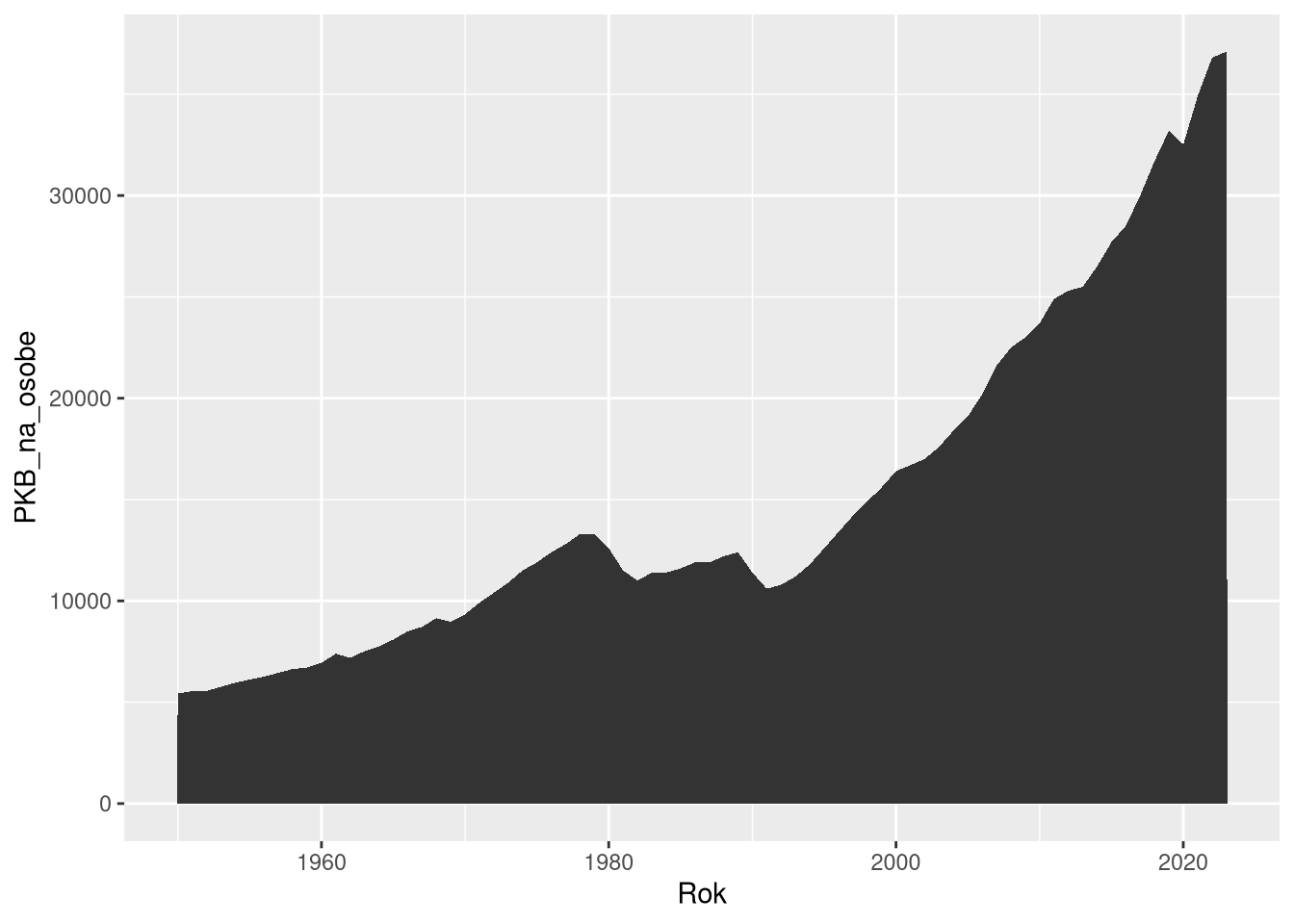

5.4.3.3 Statystyki

Czy chcemy przedstawić dane bezpośrednio czy w przetworzonej postaci?

Wykresy proste to takie, w których dane nie są przetwarzane w sposób niejawny. Przykłady takich wykresów to wykresy punktowe, liniowe, słupkowe, tekstowe.

df0_2019 = filter(gm0, Rok == 2019)
head(df0_2019)

# A tibble: 6 × 8
  Kraj      Rok Region Populacja PKB_na_osobe Ocz_dl_zycia CO2_na_osobe Plodnosc
  <chr>   <dbl> <chr>      <dbl>        <dbl>        <dbl>        <dbl>    <dbl>
1 Austra…  2019 Azja      2.54e7        49400         82.9           NA     1.82
2 Brunei   2019 Azja      4.38e5        61400         74.4           NA     1.84
3 Kambod…  2019 Azja      1.62e7         4460         69.9           NA     2.47
4 Chiny    2019 Azja      1.42e9        16000         77.6           NA     1.64
5 Fidżi    2019 Azja      9.18e5        13200         68.4           NA     2.45
6 Hongko…  2019 Azja      7.5 e6        59600         84.5           NA     1.36

df1sel_2019 = filter(df1, Kraj %in% c("Polska", "Niemcy", "Francja", "Włochy", "Hiszpania"), Rok == 2019)
head(df1sel_2019)

# A tibble: 5 × 4
  Kraj        Rok Ocz_dl_zycia PKB_na_osobe
  <chr>     <dbl>        <dbl>        <dbl>
1 Francja    2019         82.9        45900
2 Niemcy     2019         81.2        53900
3 Włochy     2019         83.1        42700
4 Polska     2019         78.1        33200
5 Hiszpania  2019         83.1        40800

ggplot(df0_2019, aes(PKB_na_osobe, Ocz_dl_zycia)) + geom_point()
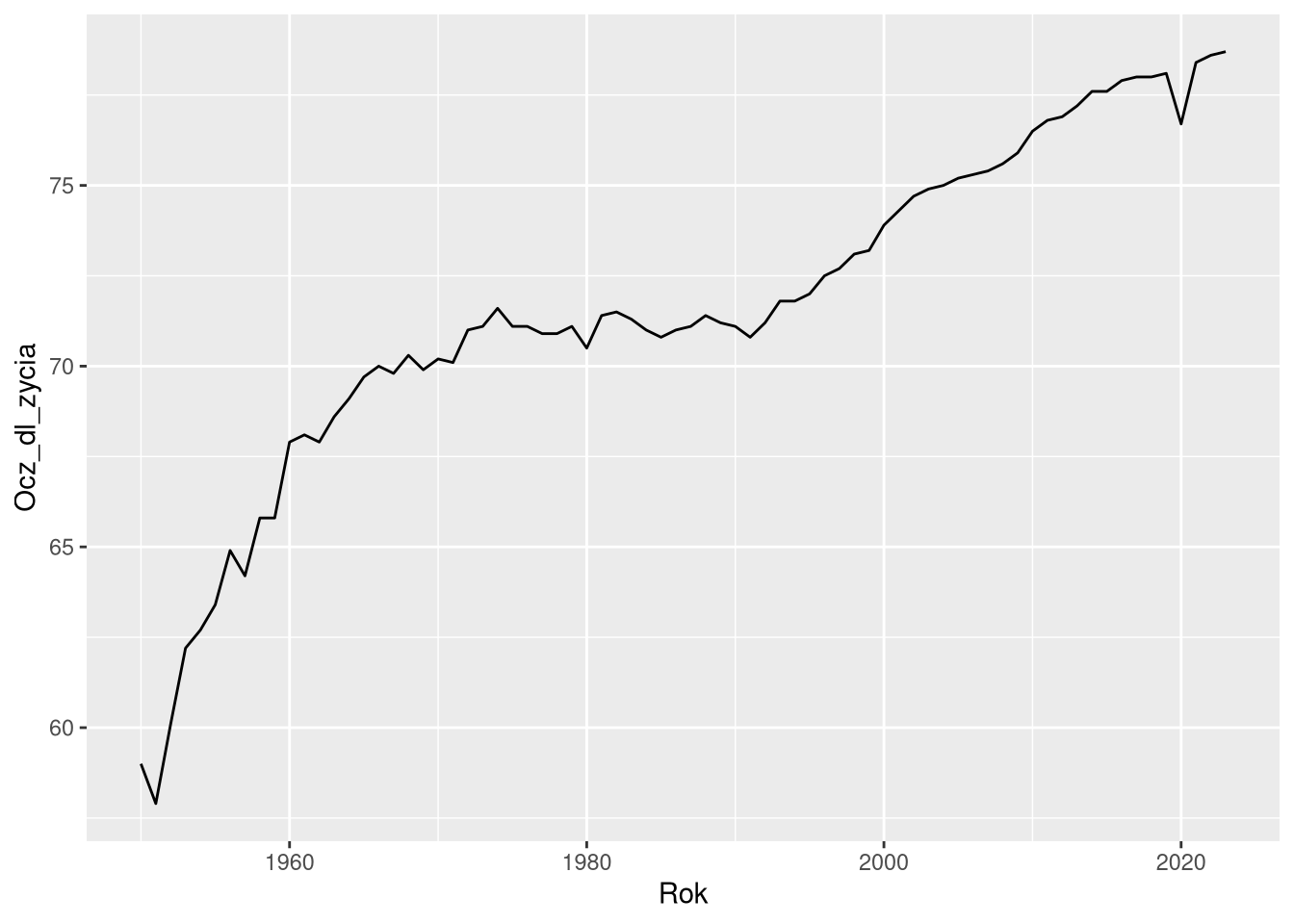
ggplot(df1pol, aes(Rok, Ocz_dl_zycia)) + geom_line()
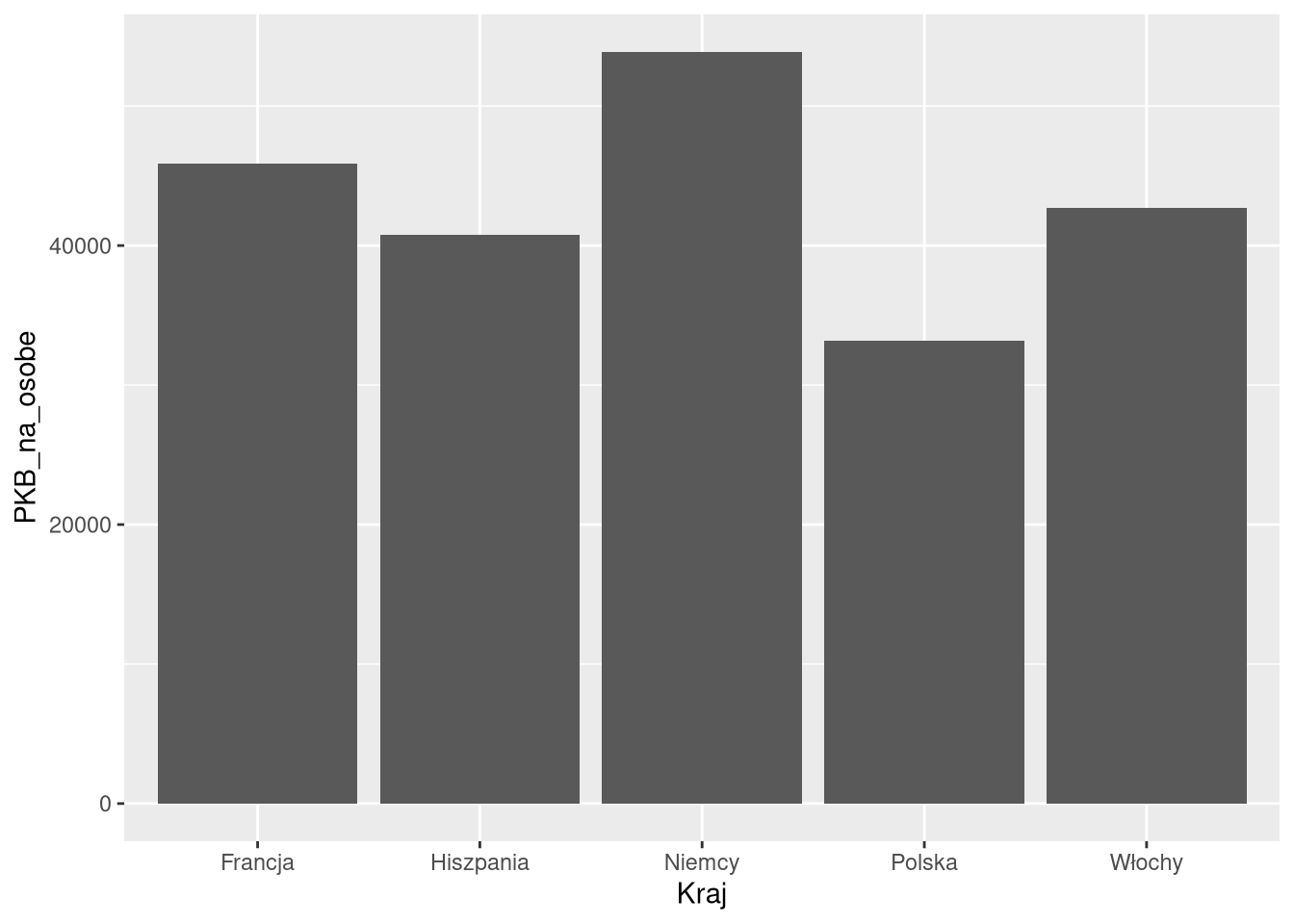
ggplot(df1sel_2019, aes(Kraj, PKB_na_osobe)) + geom_col()
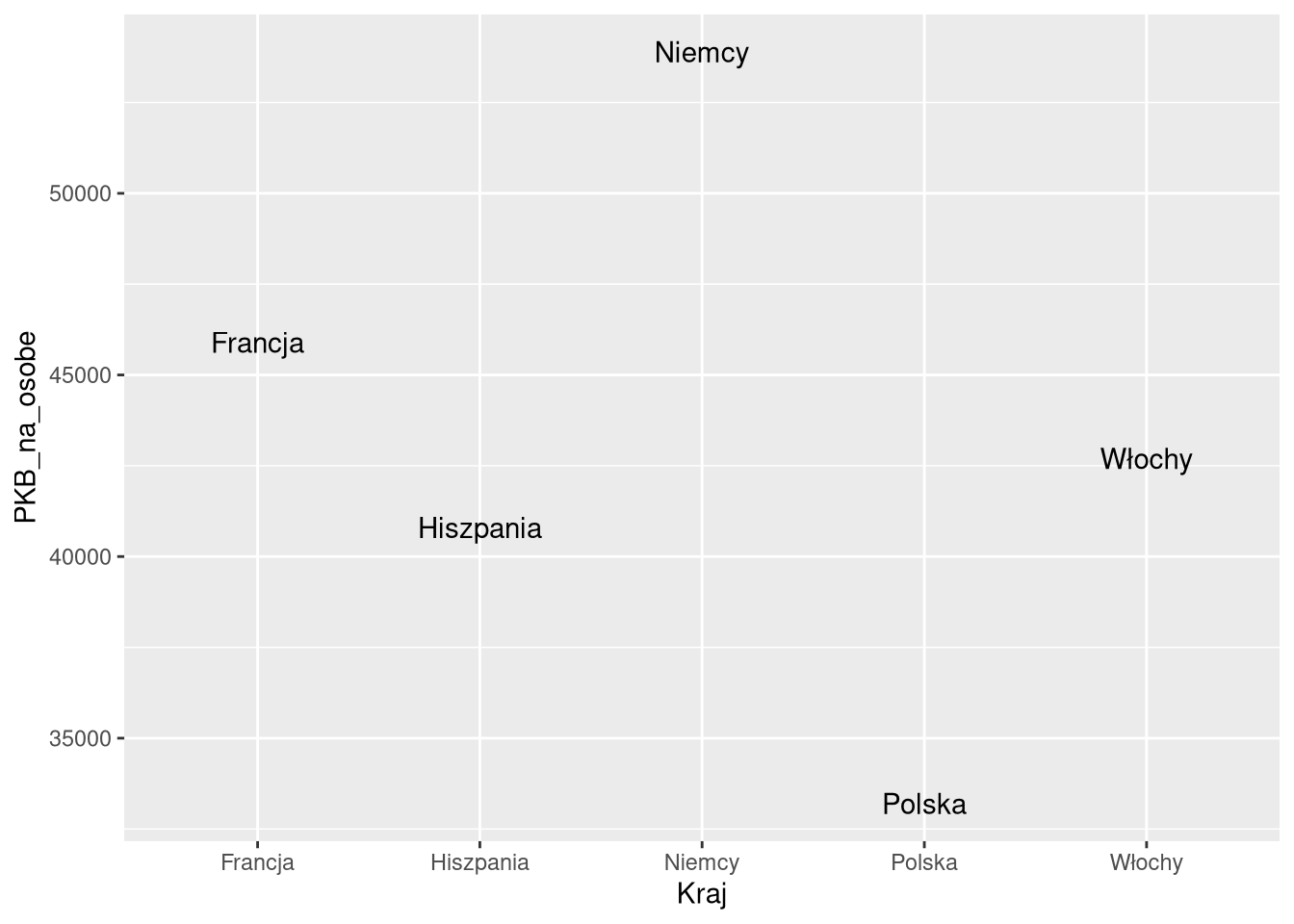
ggplot(df1sel_2019, aes(Kraj, PKB_na_osobe, label = Kraj)) + geom_text()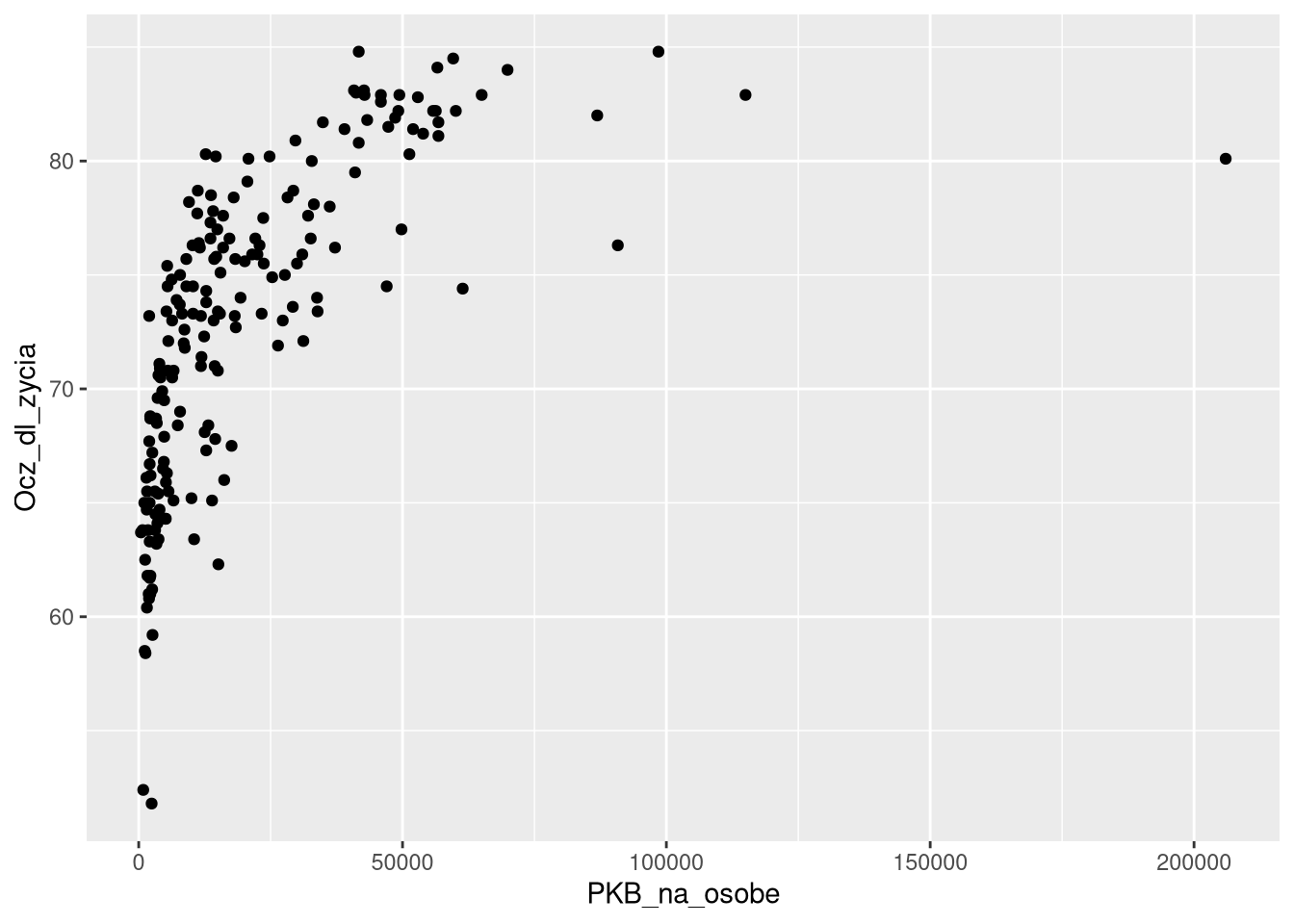

Wykresy złożone natomiast to takie, gdzie dane są przetwarzane w sposób niejawny, np. histogramy, wykresy pudełkowe, wykresy skrzypcowe, wykresy zawierające zakresy błędu/niepewności.

ggplot(df0_2019, aes(Region)) + geom_bar()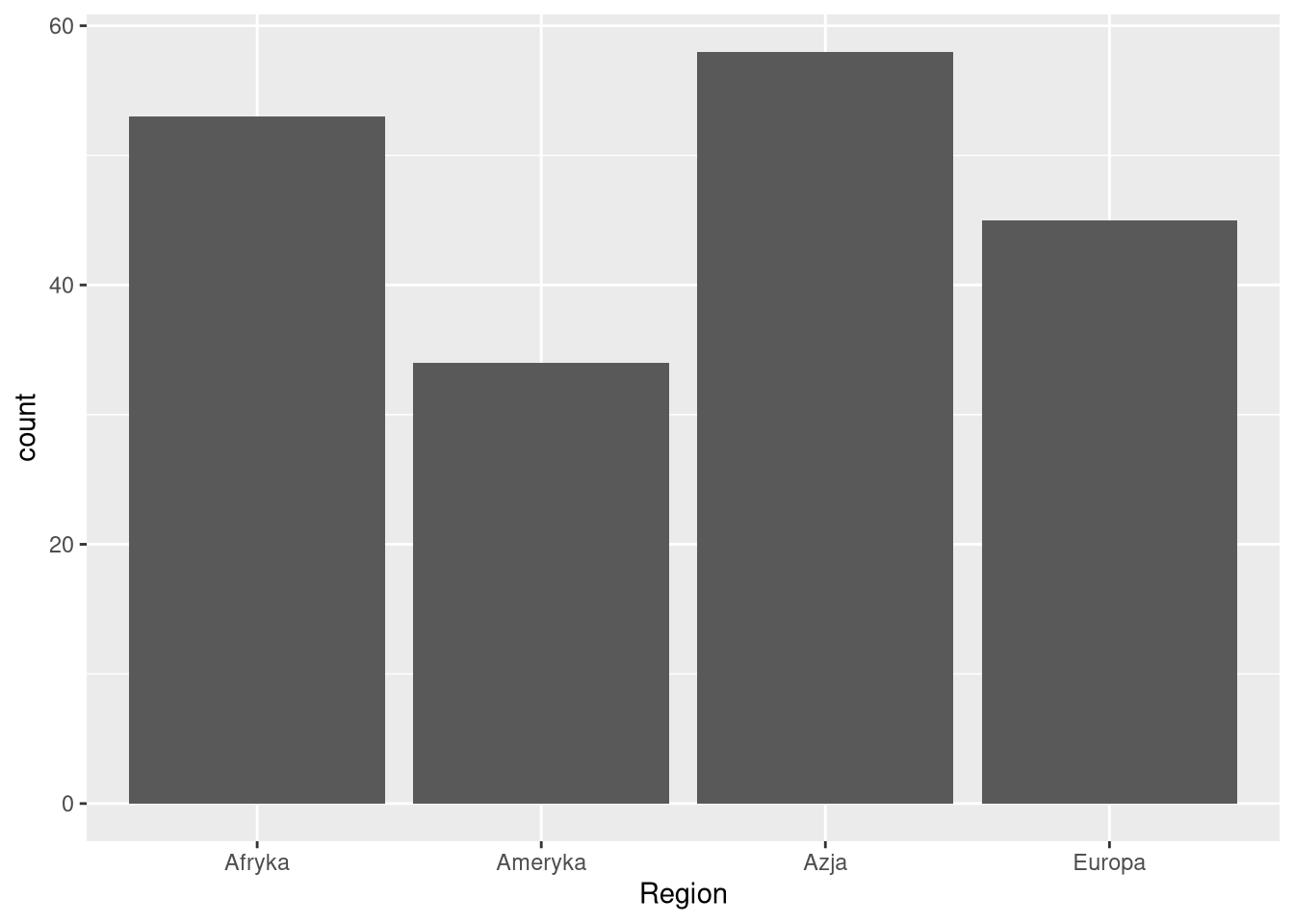

df0sel = filter(gm0, Rok == 2019)
head(df0sel)

# A tibble: 6 × 8
  Kraj      Rok Region Populacja PKB_na_osobe Ocz_dl_zycia CO2_na_osobe Plodnosc
  <chr>   <dbl> <chr>      <dbl>        <dbl>        <dbl>        <dbl>    <dbl>
1 Austra…  2019 Azja      2.54e7        49400         82.9           NA     1.82
2 Brunei   2019 Azja      4.38e5        61400         74.4           NA     1.84
3 Kambod…  2019 Azja      1.62e7         4460         69.9           NA     2.47
4 Chiny    2019 Azja      1.42e9        16000         77.6           NA     1.64
5 Fidżi    2019 Azja      9.18e5        13200         68.4           NA     2.45
6 Hongko…  2019 Azja      7.5 e6        59600         84.5           NA     1.36

ggplot(df0sel, aes(Region, Ocz_dl_zycia)) + geom_boxplot()
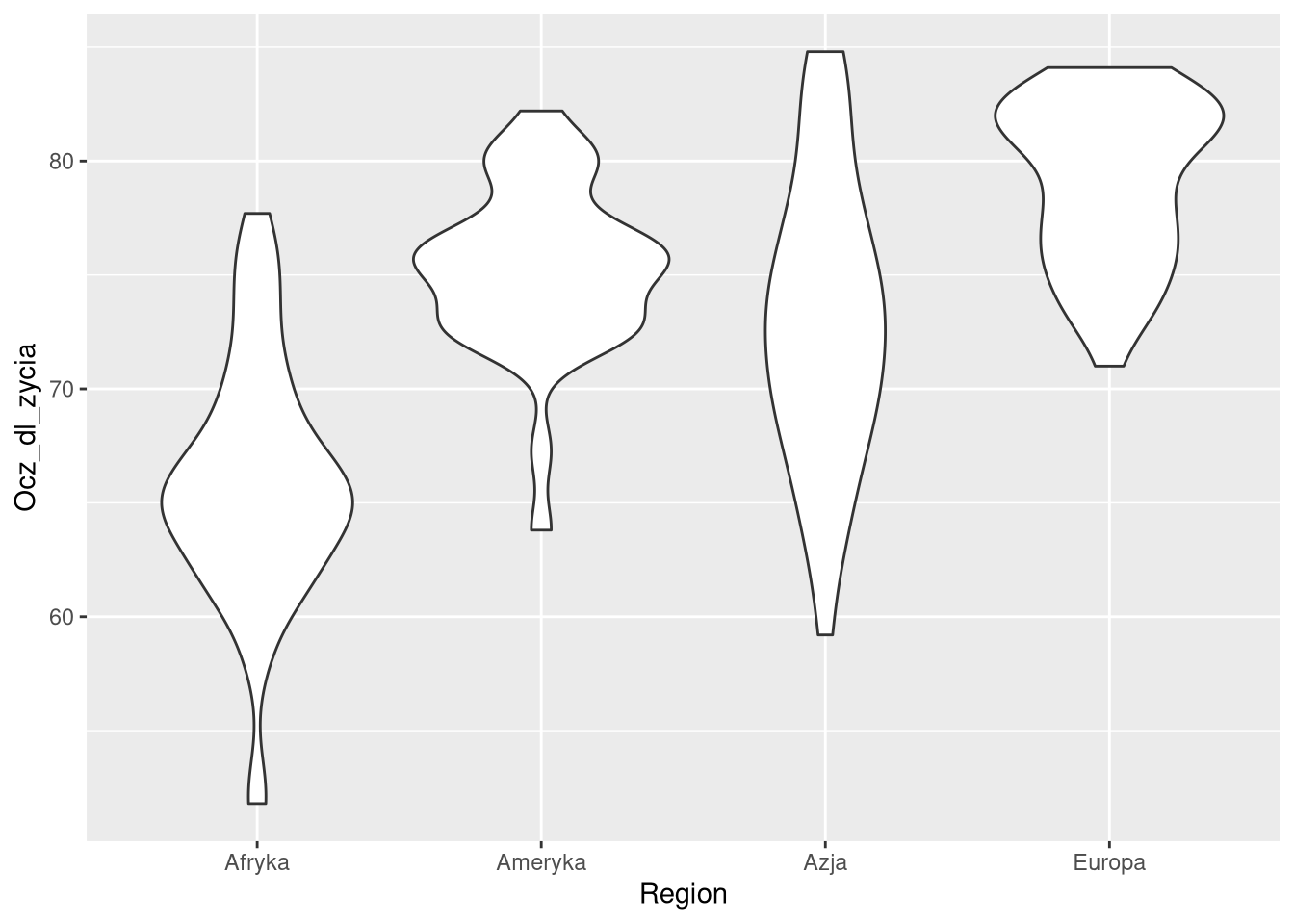
ggplot(df0sel, aes(Region, Ocz_dl_zycia)) + geom_violin()
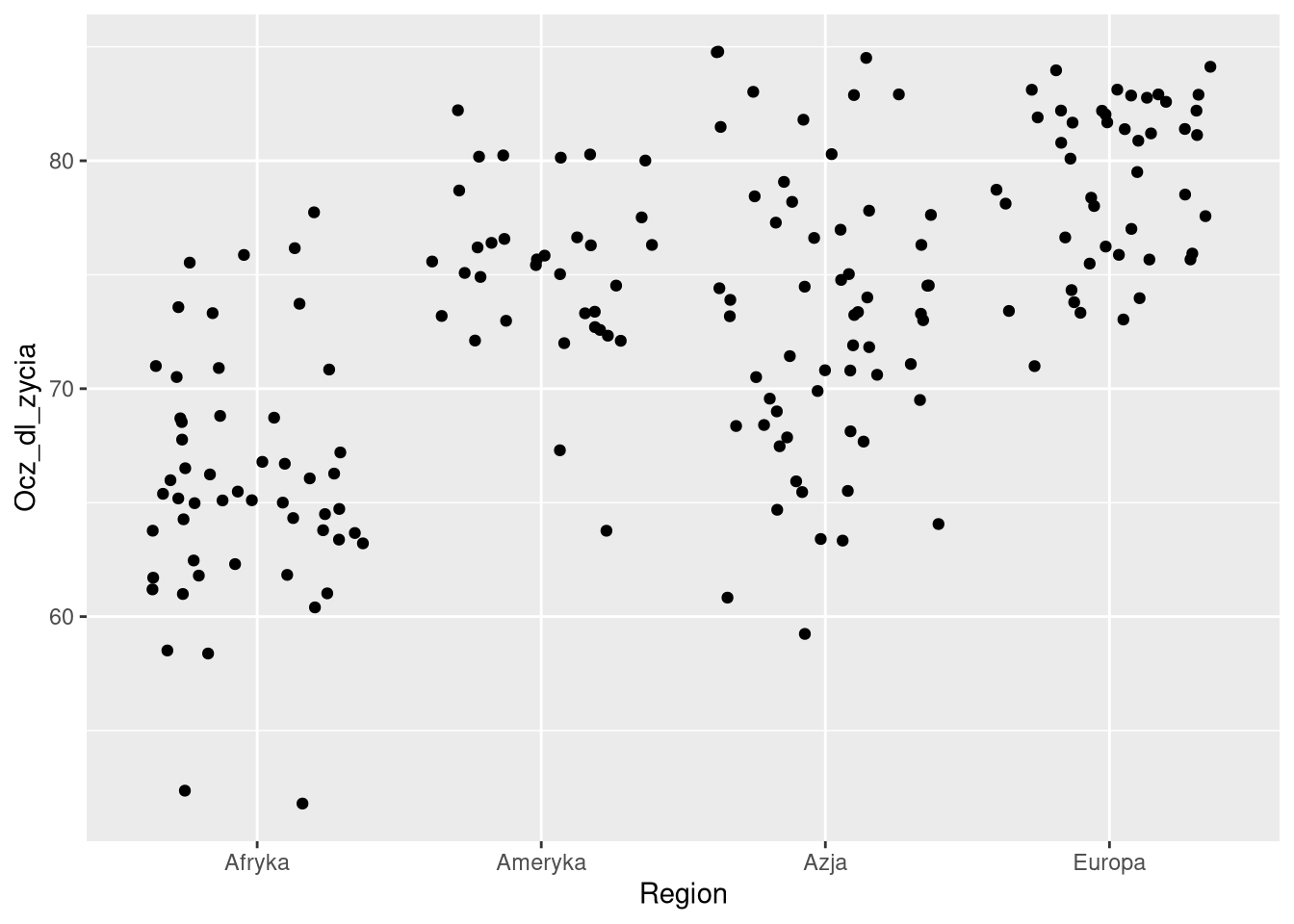
ggplot(df0sel, aes(Region, Ocz_dl_zycia)) + geom_jitter()
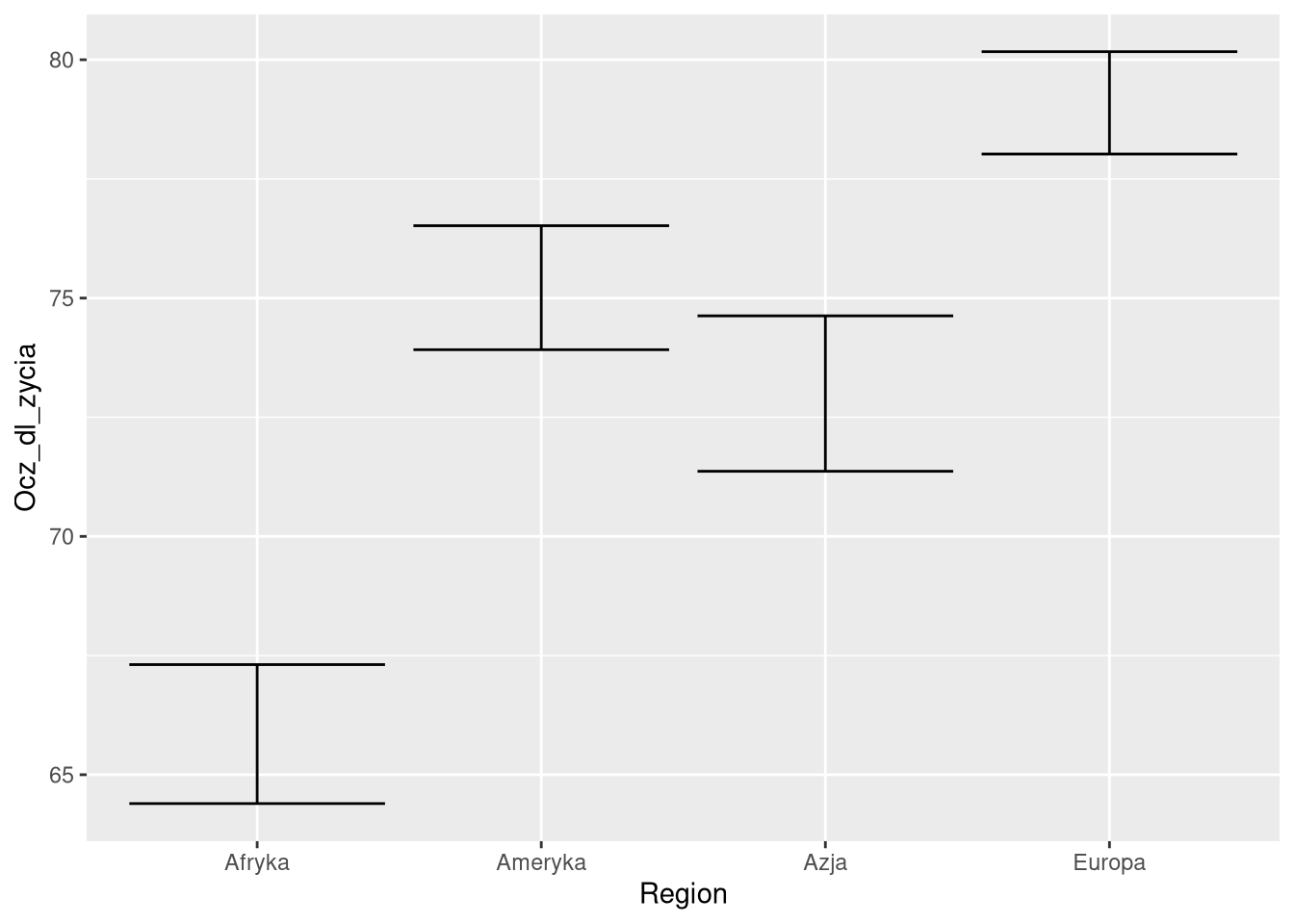
ggplot(df0sel, aes(Region, Ocz_dl_zycia)) + stat_summary(fun.data = "mean_cl_normal", geom = "errorbar")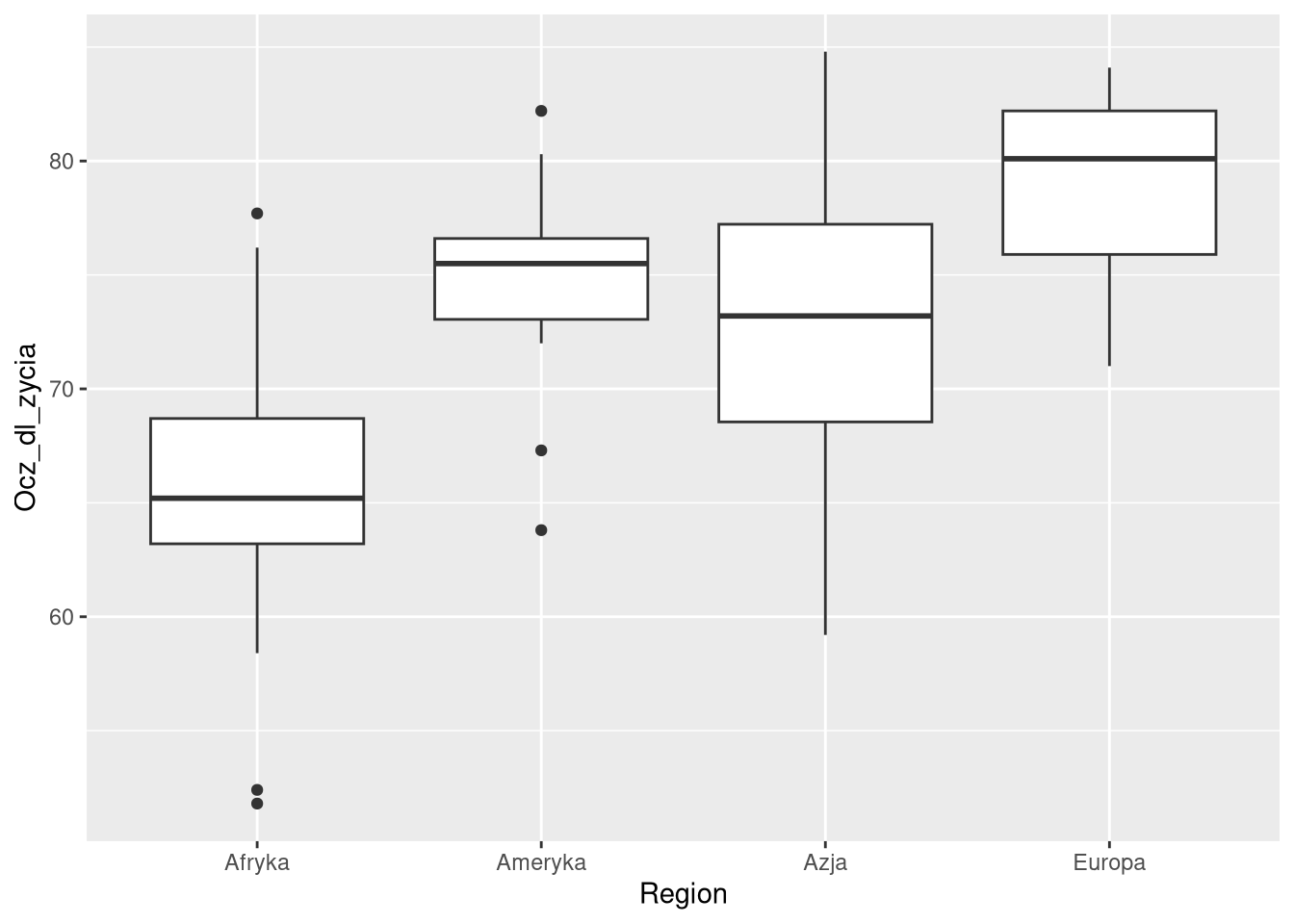 

5.4.3.4 Przesunięcia

Czy geometrie wymagają przesunięcia?

W przypadku punktów, szczególnie należących do tej samej kategorii, mogą one na siebie nachodzić. Taka sytuacja może być rozwiązana za pomocą przesunięcia punktów, np. za pomocą przesunięcia (ang. position) "jitter".

ggplot(df0sel, aes(Region, Ocz_dl_zycia)) + geom_point(position = "identity")
ggplot(df0sel, aes(Region, Ocz_dl_zycia)) + geom_point(position = "jitter")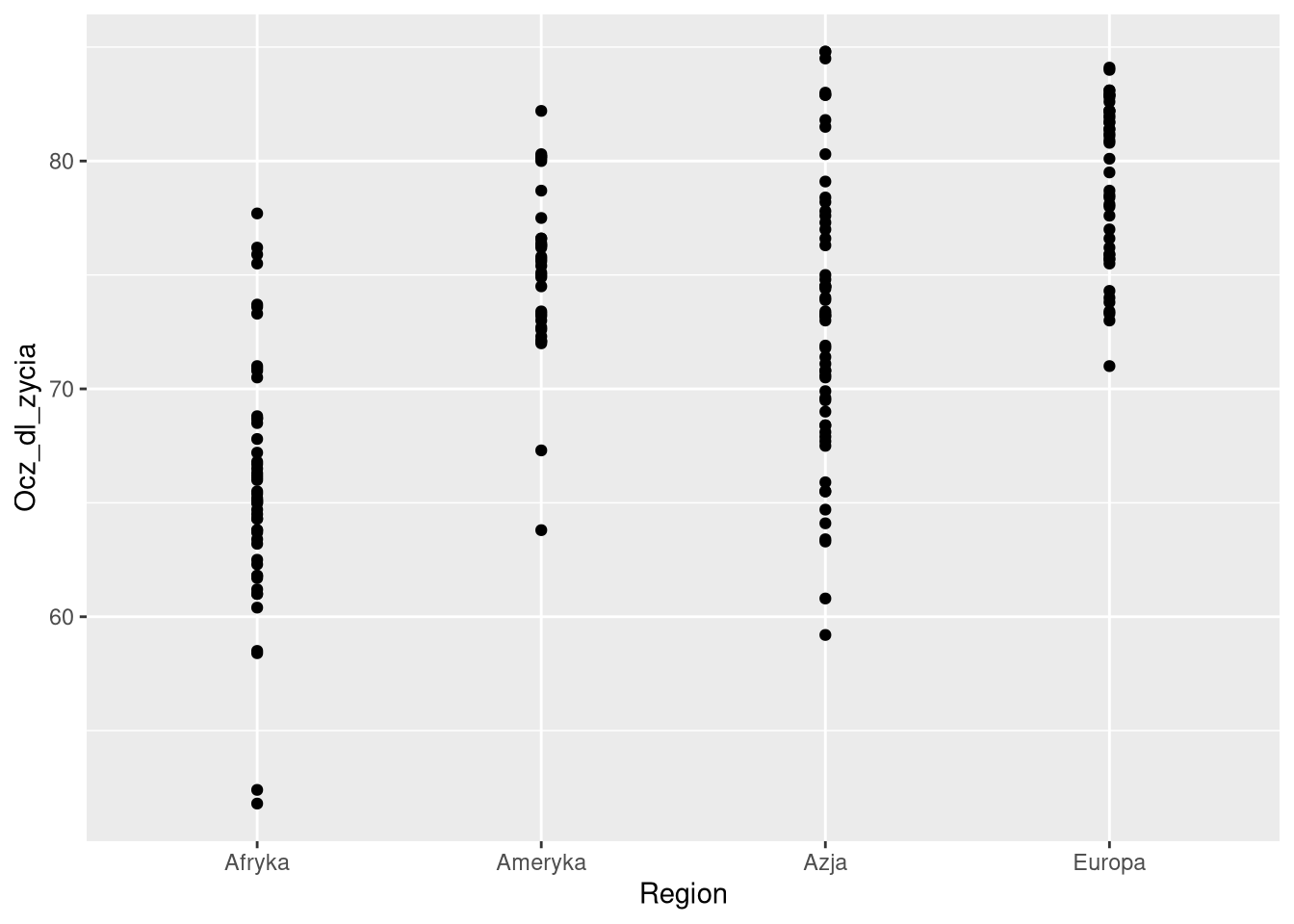

Przesunięcia pozwalają na lepsze porównanie wartości między kategoriami oraz na dokładniejsze określenie ich liczby.

df1sel_1920 = filter(df1, Kraj %in% c("Polska", "Niemcy", "Francja", "Włochy", "Hiszpania"), Rok %in% c(2019, 2020))
head(df1sel_1920)

# A tibble: 6 × 4
  Kraj      Rok Ocz_dl_zycia PKB_na_osobe
  <chr>   <dbl>        <dbl>        <dbl>
1 Francja  2019         82.9        45900
2 Francja  2020         82.2        42200
3 Niemcy   2019         81.2        53900
4 Niemcy   2020         81          51800
5 Włochy   2019         83.1        42700
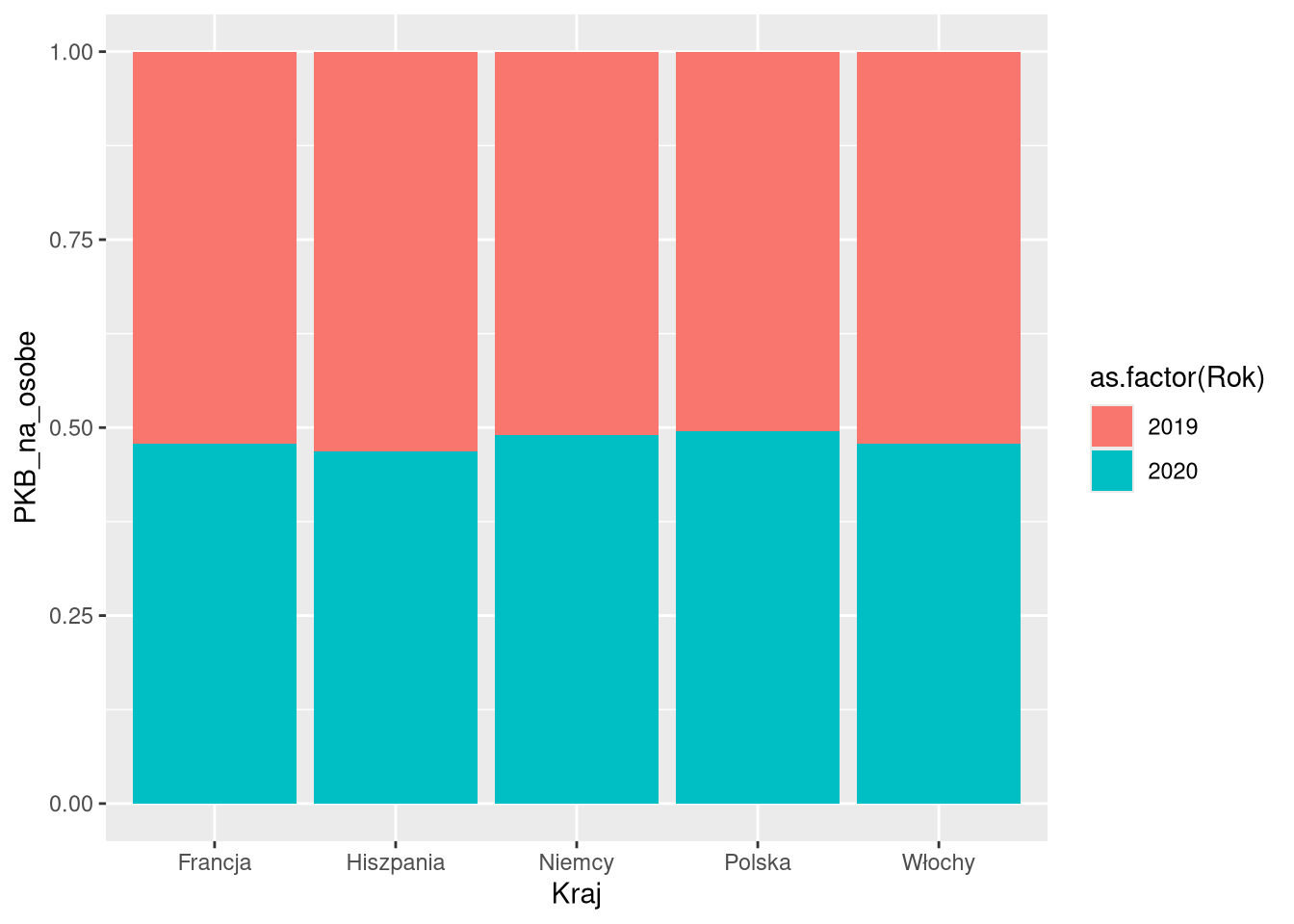
6 Włochy   2020         81.9        39100

Przesunięcia umożliwiają również różnorodne wizualizacje danych używając tej samej formy. Poniższe cztery przykłady pokazują różne przesunięcia dla tych samych danych i tej samej formy (geom_col). Pierwsze z nich to domyślne przesunięcie ("stack"), gdzie słupki dla kolejnych kategorii są ustawione jeden na drugim. Drugi i trzeci przykład to przesunięcia "dodge" i "dodge2", gdzie słupki są ustawione obok siebie. Ostatni przykład to przesunięcie "fill", gdzie słupki dla kolejnych kategorii są ustawione jeden na drugim, ale wysokość każdego z nich jest ustawiona na 1.

ggplot(df1sel_1920, aes(Kraj, PKB_na_osobe, fill = as.factor(Rok))) + 
    geom_col(position = "stack")
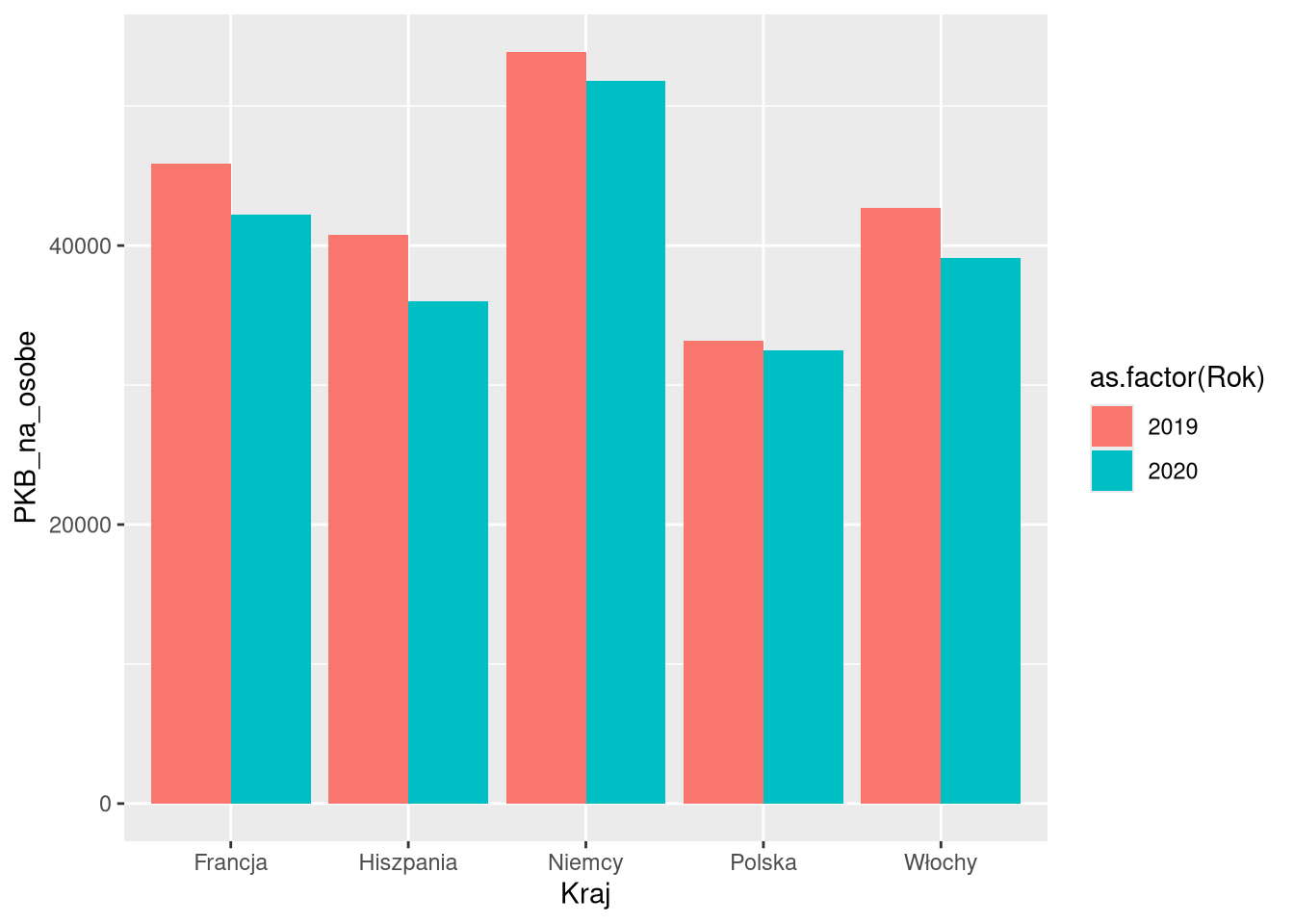
ggplot(df1sel_1920, aes(Kraj, PKB_na_osobe, fill = as.factor(Rok))) +
    geom_col(position = "dodge")
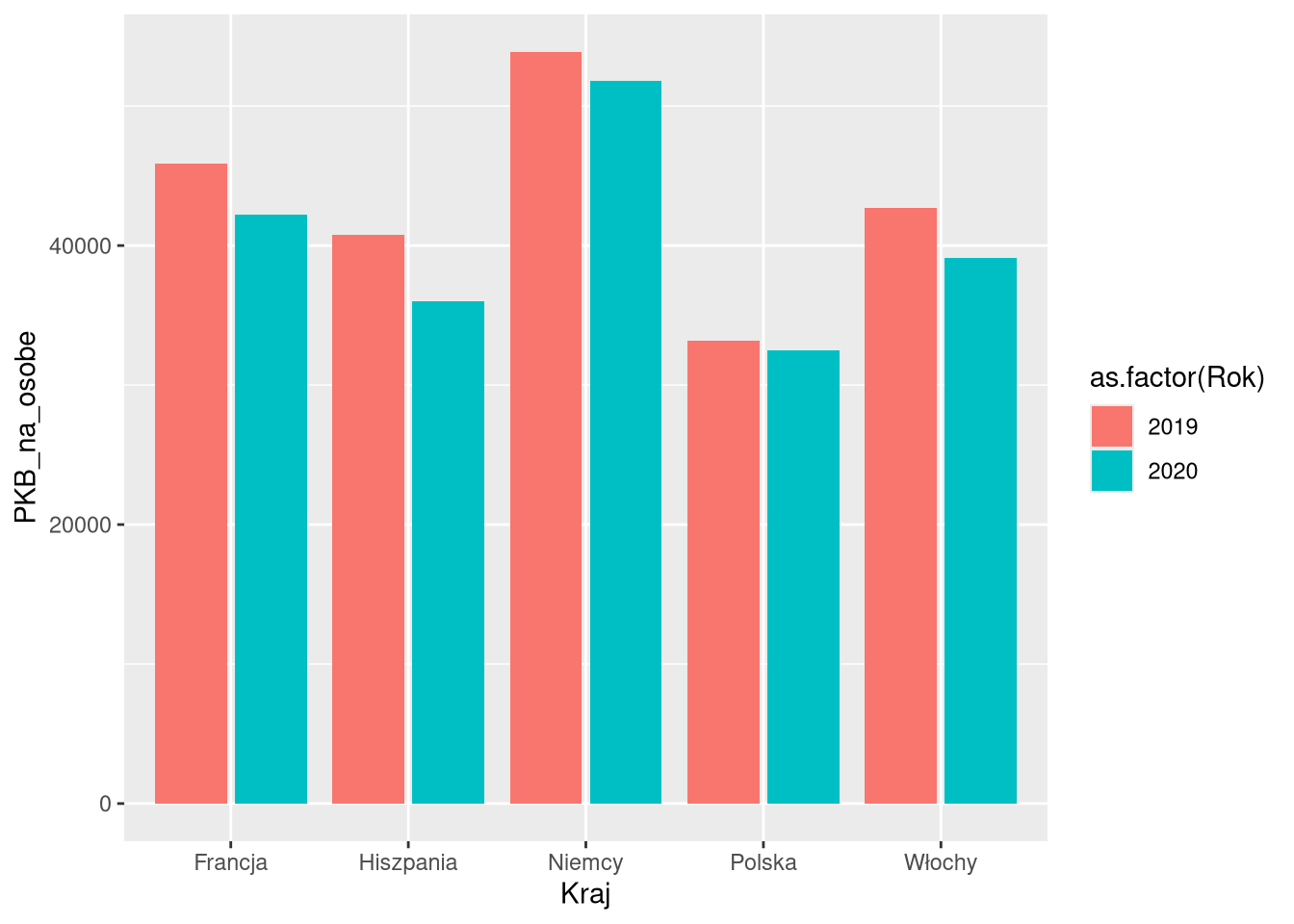
ggplot(df1sel_1920, aes(Kraj, PKB_na_osobe, fill = as.factor(Rok))) + 
    geom_col(position = "dodge2")
ggplot(df1sel_1920, aes(Kraj, PKB_na_osobe, fill = as.factor(Rok))) + 
    geom_col(position = "fill")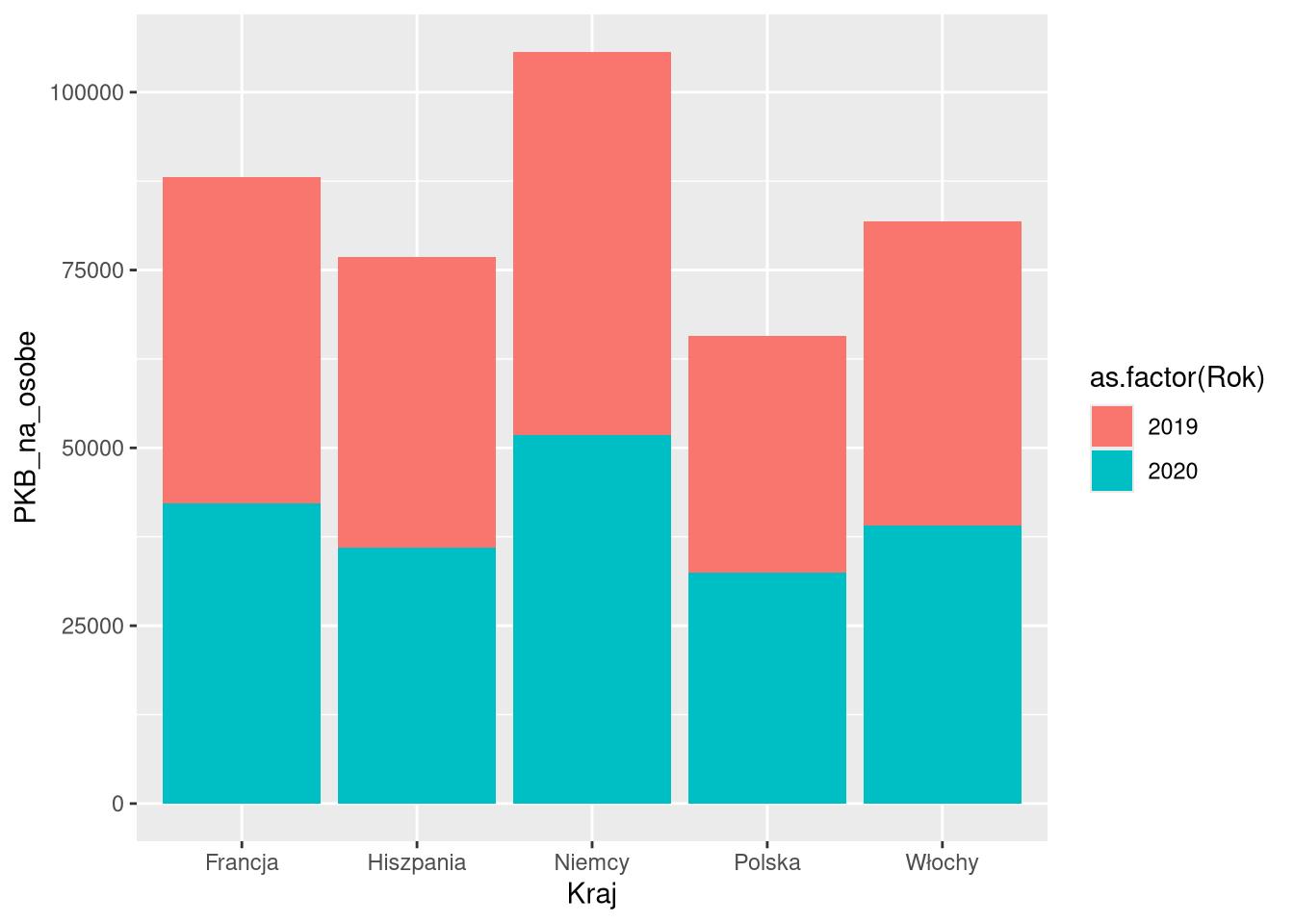

df1sel = filter(df1, Kraj %in% c("Polska", "Niemcy", "Francja", "Włochy", "Hiszpania"))
df1sel$Rok = df1sel$Rok
head(df1sel)

# A tibble: 6 × 4
  Kraj      Rok Ocz_dl_zycia PKB_na_osobe
  <chr>   <dbl>        <dbl>        <dbl>
1 Francja  1950         67.1        11400
2 Francja  1951         66.7        11900
3 Francja  1952         68.1        12100
4 Francja  1953         68.5        12300
5 Francja  1954         69          12800
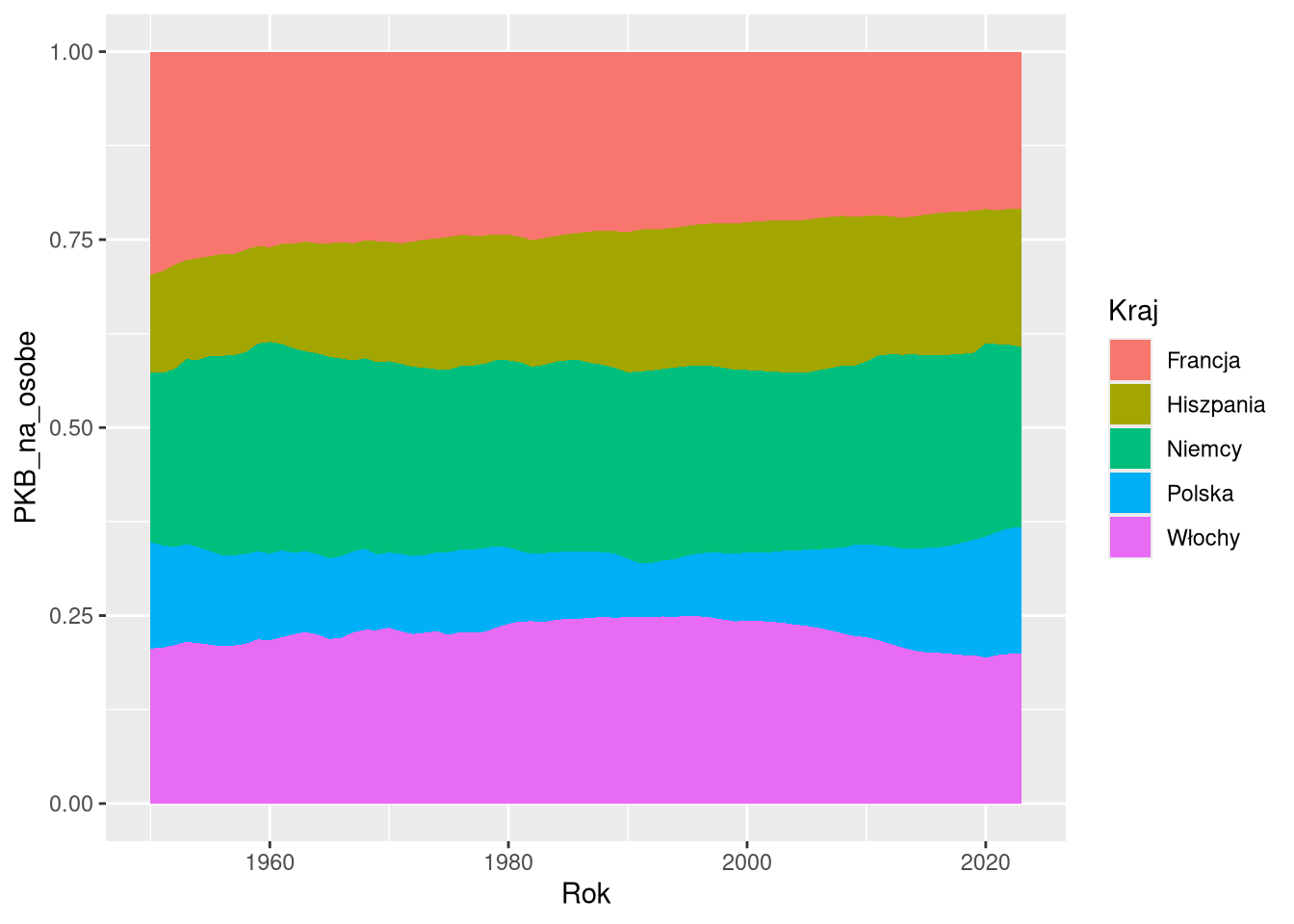
6 Francja  1955         69.3        13400

Przesunięcia mają także zastosowanie do innego rodzaju form, np. do wykresów powierzchniowych (geom_area). W pierwszym przykładzie przesunięcie "identity" oznacza, że obszary są nakładane na siebie. W takiej sytuacji często stosuje się przezroczystość, aby lepiej zobaczyć obszary dla poszczególnych kategorii i porównać je między sobą. Drugi przykład to przesunięcie "stack", gdzie obszary są ustawione jeden na drugim. Pozwala to lepiej zobaczyć ogólny wzrost lub spadek wartości. Ostatni przykład to przesunięcie "fill", gdzie obszary są ustawione jeden na drugim, ale ich wysokość jest ustawiona na 1. Takie ustawienie pozwala na porównanie udziału poszczególnych kategorii w całości danych.

ggplot(df1sel, aes(Rok, PKB_na_osobe, fill = Kraj)) + 
    geom_area(position = "identity") #, alpha = 0.1
ggplot(df1sel, aes(Rok, PKB_na_osobe, fill = Kraj)) + 
    geom_area(position = "stack")
ggplot(df1sel, aes(Rok, PKB_na_osobe, fill = Kraj)) + 
    geom_area(position = "fill")

5.4.4 Miary

W jaki sposób tranformujemy cechy obserwacji na ich przedstawienie na wykresie?

Miary (ang. scales) to transformacje zmiennych, które pozwalają na ich przedstawienie na wykresie. Obejmuje to, między innymi, miary powiązane z kolorami, wypełnieniami, wielkościami, itd.

Dla różnego typu zmiennych istnieją wbudowane palety kolorów, które można wykorzystać w wykresach. Kolory można również ręcznie przypisywać do kategorii.

df0_1920a = filter(gm0, Rok %in% c(2019, 2020), Region == "Azja")
ggplot(df0_1920a, aes(PKB_na_osobe, Ocz_dl_zycia, color = as.factor(Rok))) + 
    geom_point()
ggplot(df0_1920a, aes(PKB_na_osobe, Ocz_dl_zycia, color = as.factor(Rok))) +
    geom_point() +
    scale_color_manual(values = c("red", "blue"))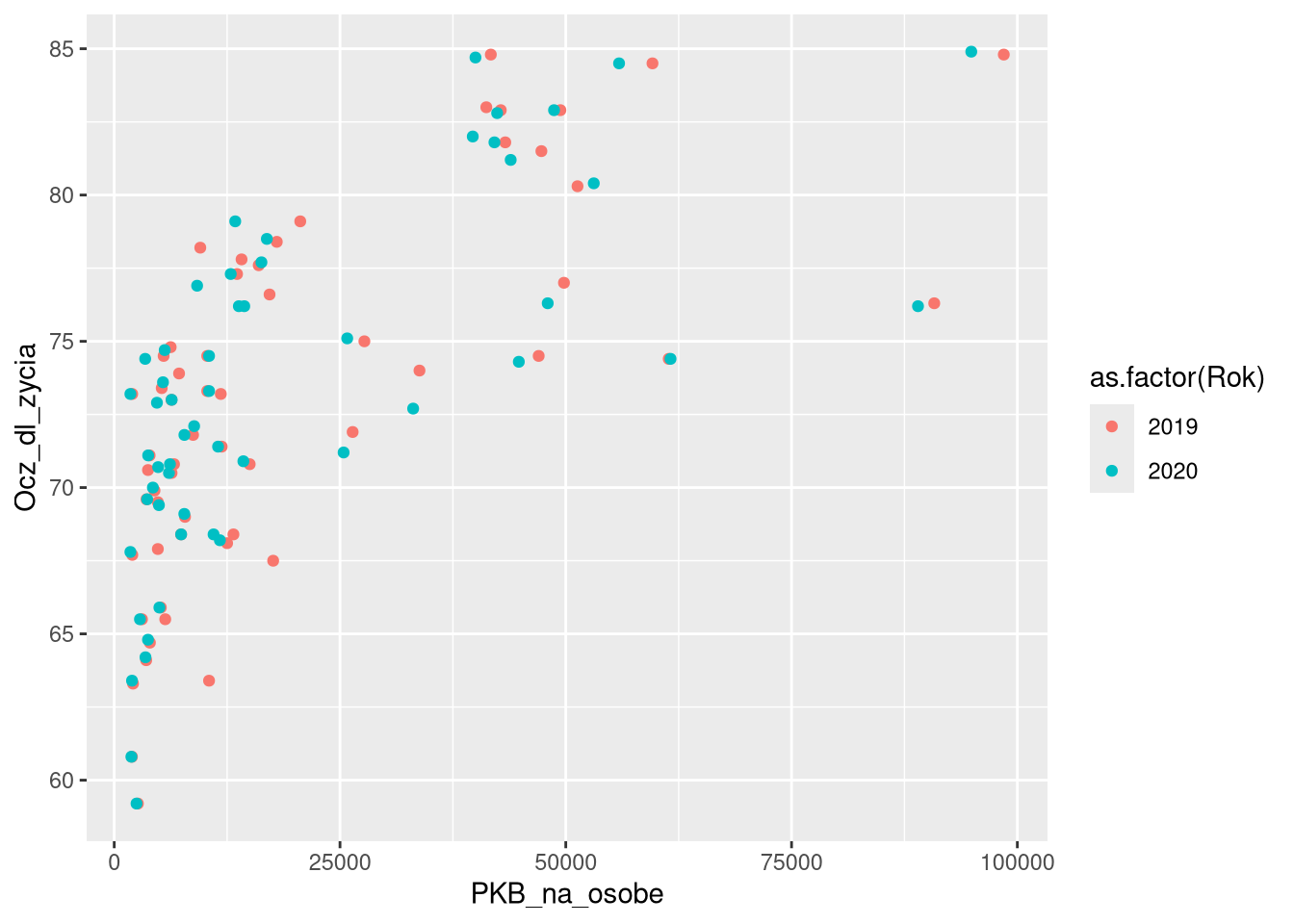

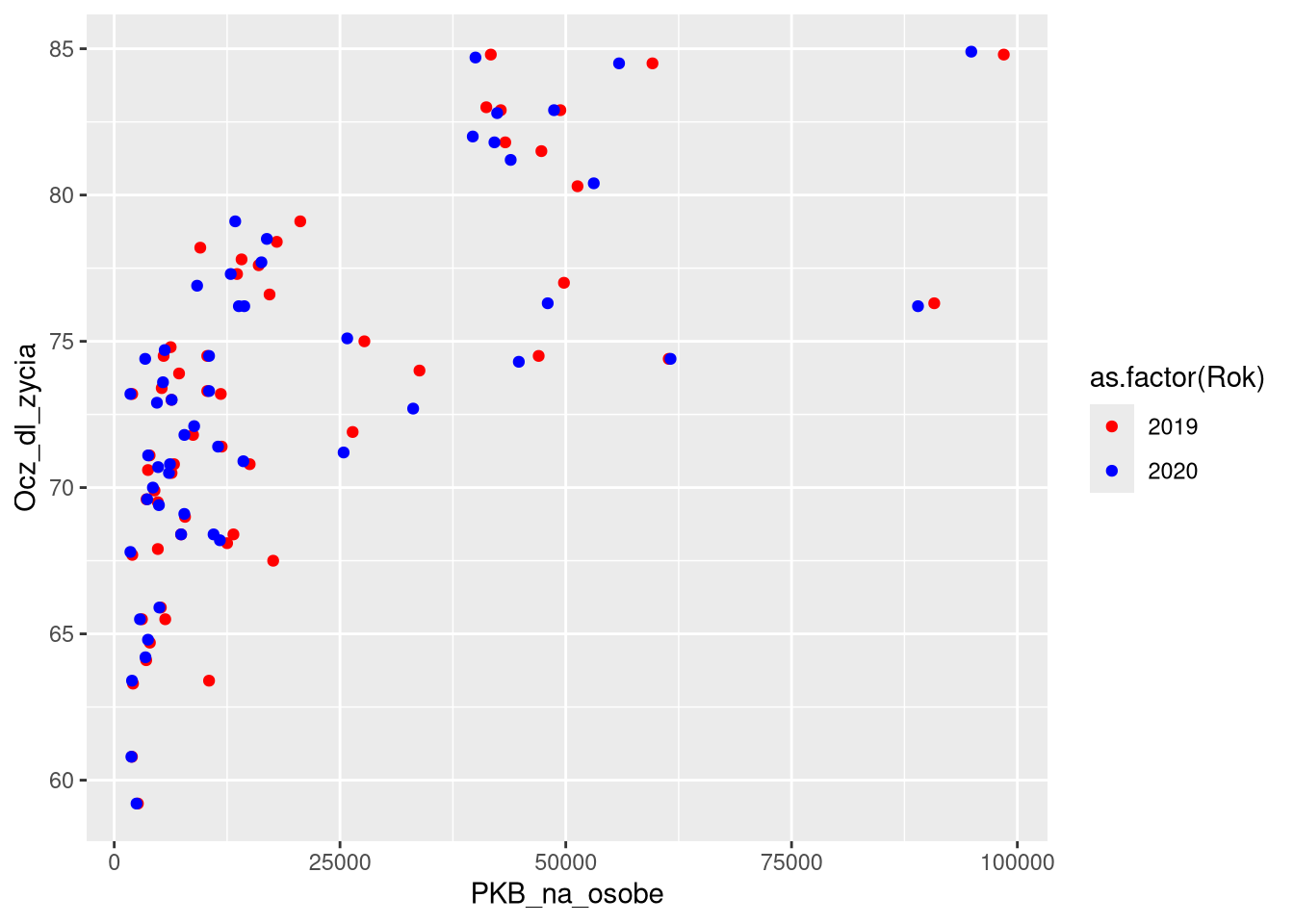
Często jednak lepszą opcją jest użycie istniejącej palety kolorów. Trzeba jednocześnie zdawać sobie sprawę z rozróżnienia między miarą koloru (ang. color) a miarą wypełnienia (ang. fill). Pierwsza z nich dotyczy koloru obwódki punktu czy koloru linii, a druga wypełnienia punktu czy powierzchni.

library(colorspace)
ggplot(df0_1920a, aes(PKB_na_osobe, Ocz_dl_zycia, color = as.factor(Rok))) + geom_point() +
    scale_color_discrete_qualitative(palette = "Dark2")
ggplot(df1sel, aes(Rok, PKB_na_osobe, fill = Kraj)) + 
    geom_area(position = "fill") +
    scale_fill_discrete_qualitative(palette = "Dark2")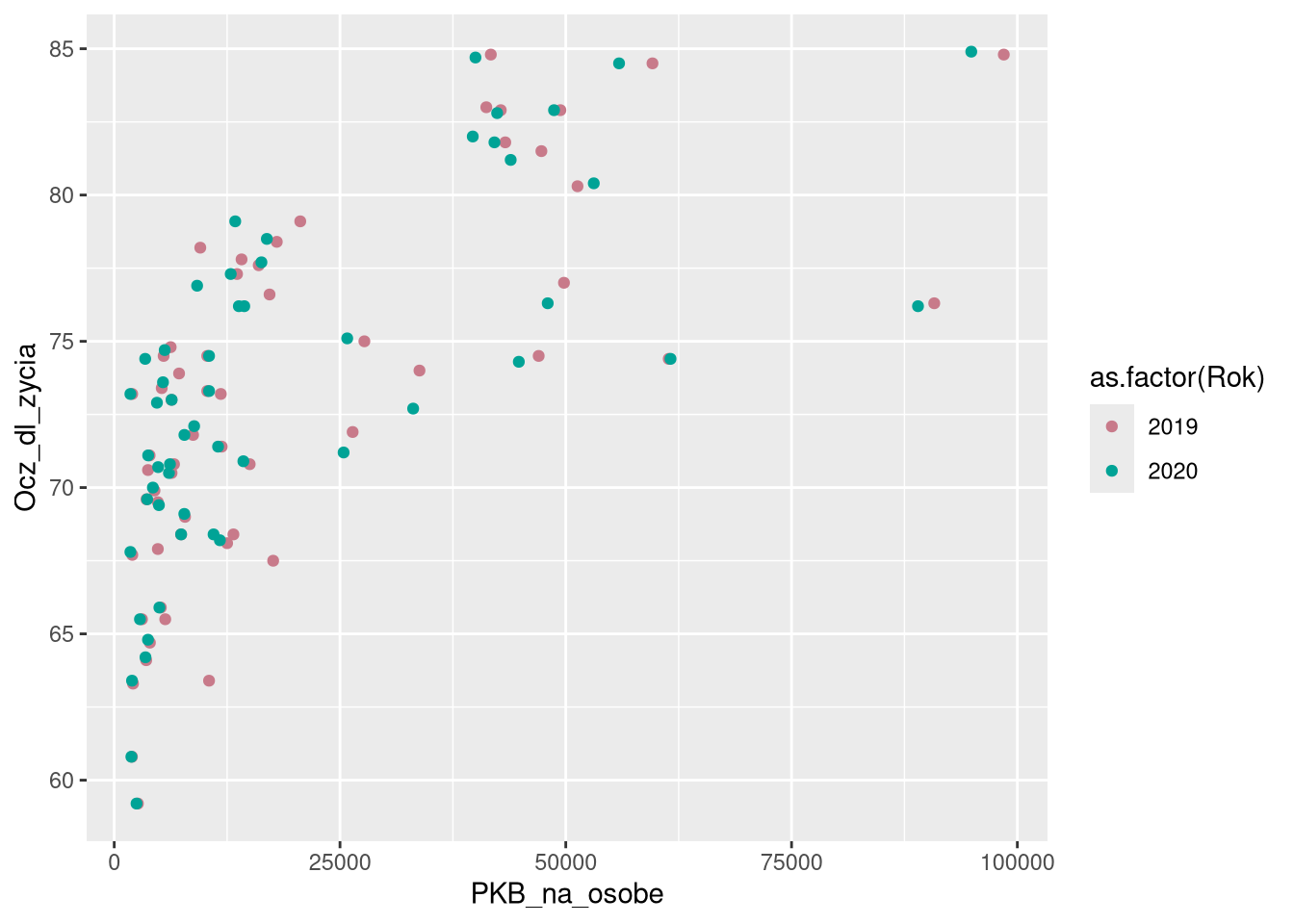

Miara wielkości (ang. size) pozwala na zmianę wielkości punktów na wykresie.

ggplot(df0_1920a, aes(PKB_na_osobe, Ocz_dl_zycia, size = Populacja)) + 
    geom_point(shape = 21) +
    scale_size()
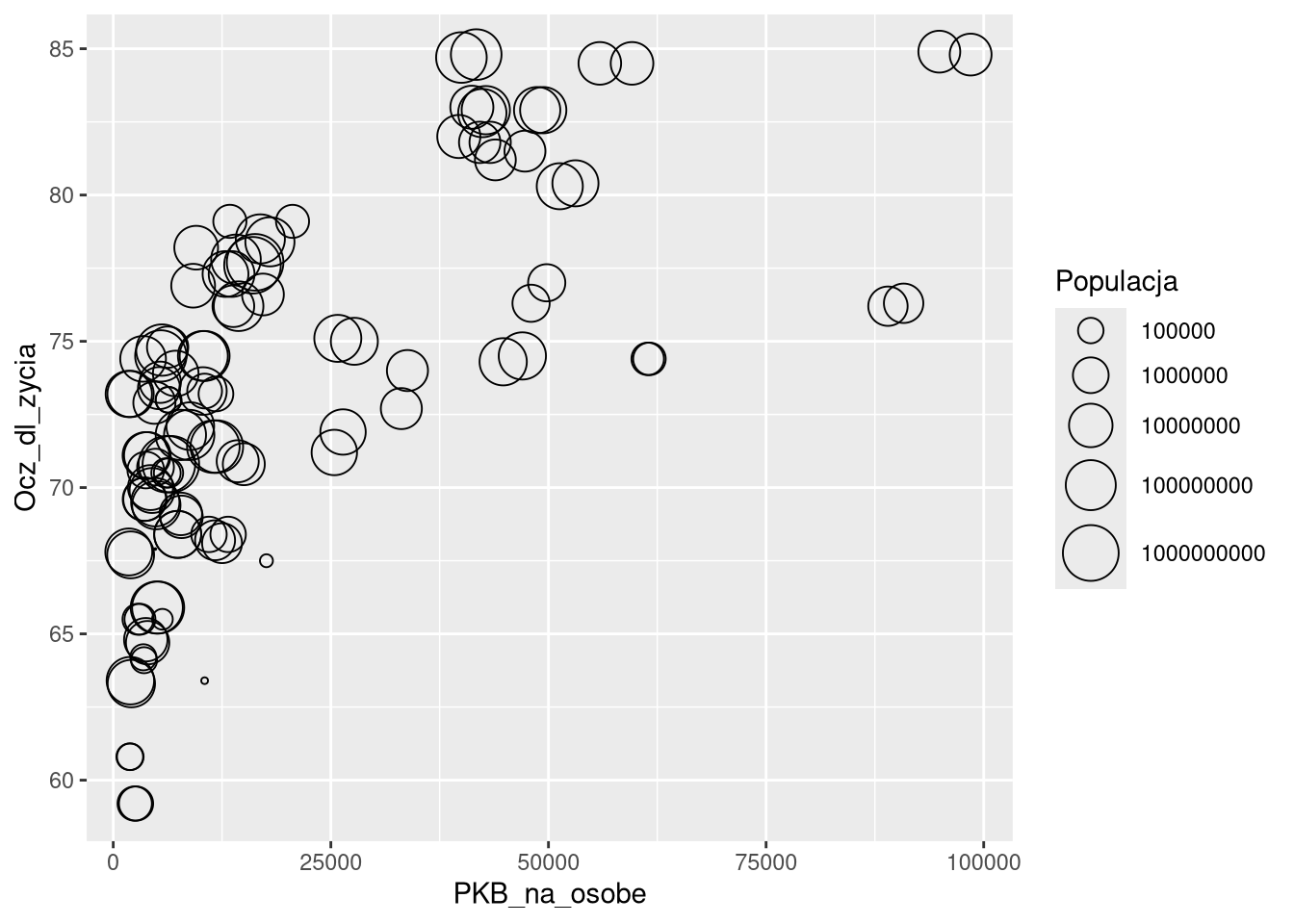
options(scipen = 999)
ggplot(df0_1920a, aes(PKB_na_osobe, Ocz_dl_zycia, size = Populacja)) + 
    geom_point(shape = 21) +
    scale_size(range = c(0, 10), trans = "log10")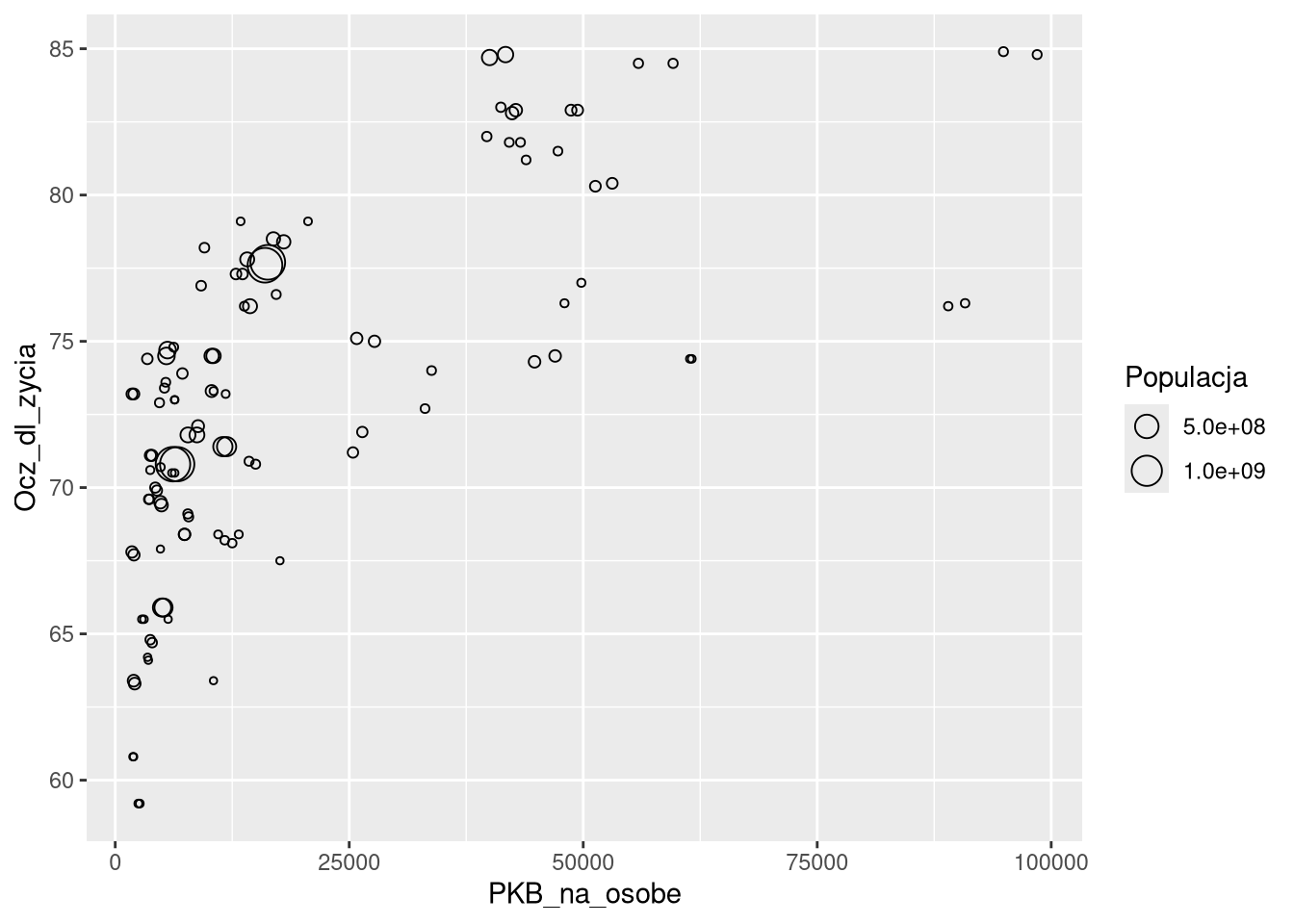

Miara kształtu (ang. shape) pozwala na zmianę kształtu punktów na wykresie na podstawie istniejących kategorii.

ggplot(df0_1920a, aes(PKB_na_osobe, Ocz_dl_zycia, shape = as.factor(Rok))) + geom_point() +
    scale_shape_manual(values = c(1, 5))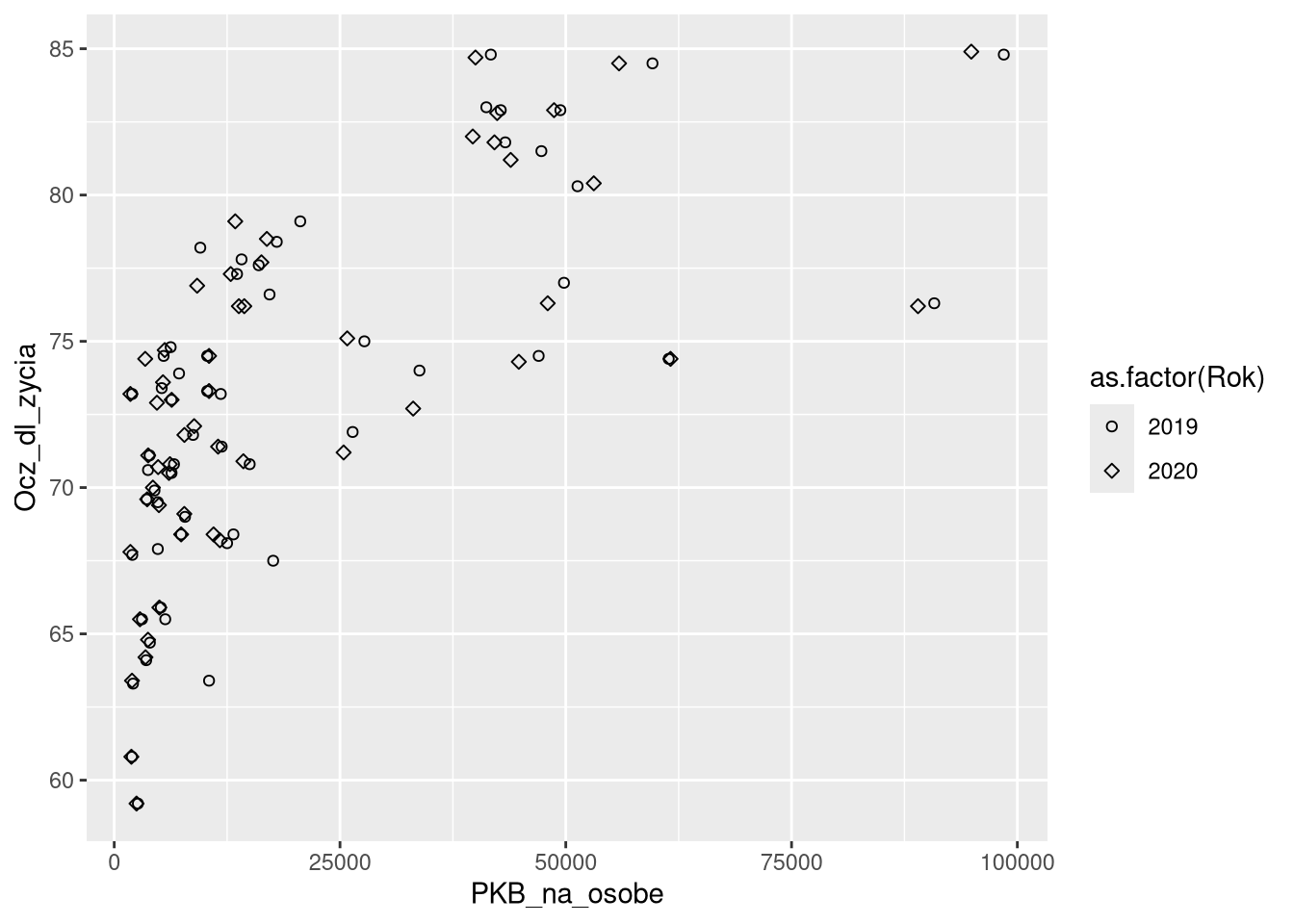

5.4.5 Układ współrzędnych

Jak określamy położenie elementów na wykresie?

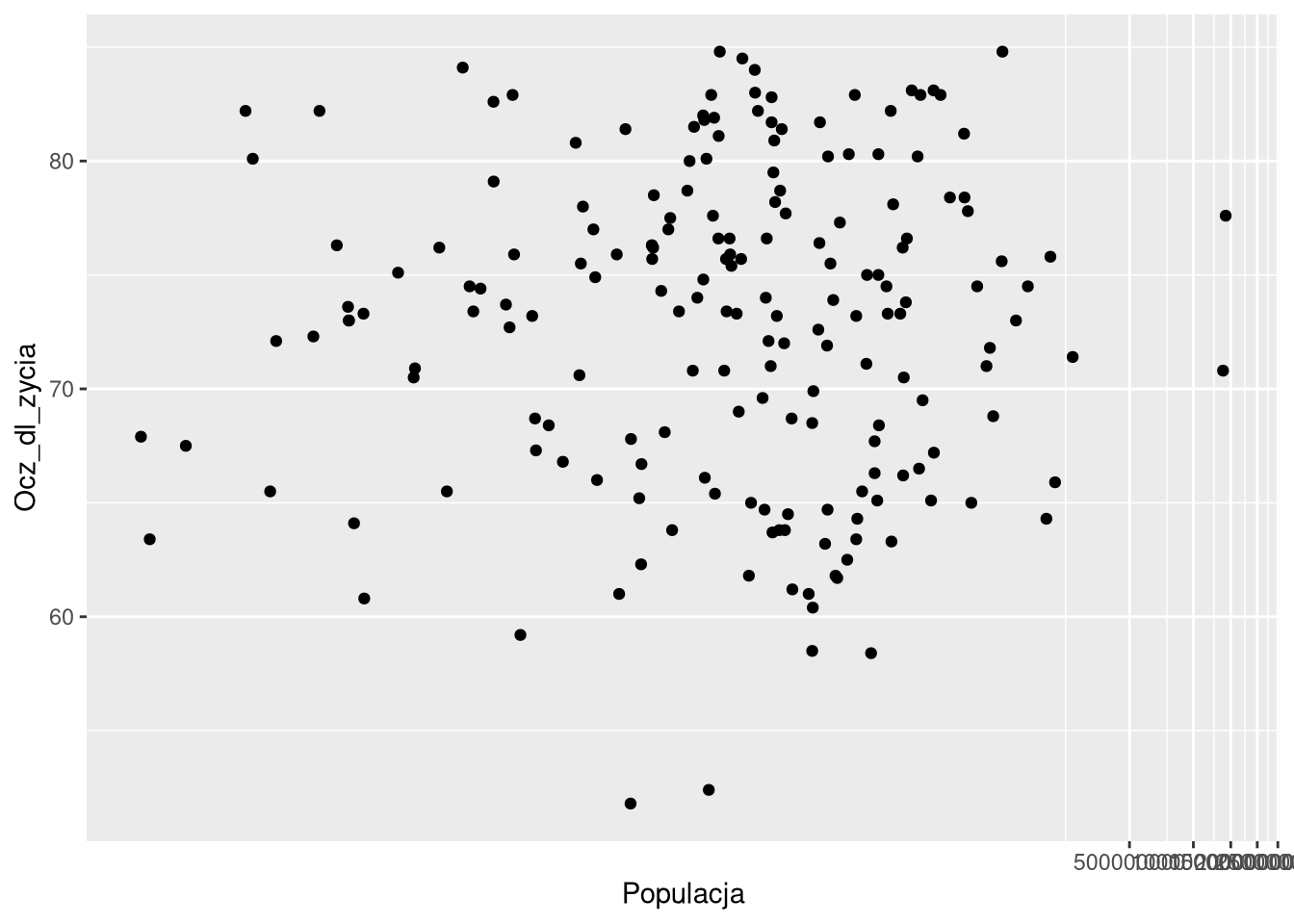
W sytacjach, gdy istnieją pojedyncze wartości wysokie lub niskie, ich bezpośrednia wizualizacja może być trudna do odczytania. W takich sytuacjach można zastosować transformację logarytmiczną czy pierwiastkową.

df0_2019 = filter(gm0, Rok == 2019)
ggplot(df0_2019, aes(x = Populacja, y = Ocz_dl_zycia)) + 
    geom_point()
ggplot(df0_2019, aes(x = Populacja, y = Ocz_dl_zycia)) +
    geom_point() +
    coord_trans(x = "log10")
ggplot(df0_2019, aes(x = Populacja, y = Ocz_dl_zycia)) +
    geom_point() +
    coord_trans(x = "sqrt")

Inna sytuacja to, gdy chcemy odwrócić osie wykresu. Taka operacja przydaje się, np. gdy chcemy ułatwić odczytanie nazw kategorii na osiach.

ggplot(df0_2019, aes(x = Region, y = Ocz_dl_zycia)) +
    geom_point() +
    coord_flip()

Domyślnie w ggplot2, wykres wypełnia całą dostępną przestrzeń. Często jest to pożądane zachowanie, ale czasami chcemy to zmienić. Przykładem takiej sytuacji jest, gdy obie osie mają taką jednostkę.

df1sel_1920_l = df0_1920a |> 
    select(Kraj, Rok, Ocz_dl_zycia) |> 
    pivot_longer(cols = Ocz_dl_zycia, names_to = "Zmienna", values_to = "Wartosc")
df1sel_1920_2 = pivot_wider(df1sel_1920_l, 
                            names_from = Rok, values_from = Wartosc)
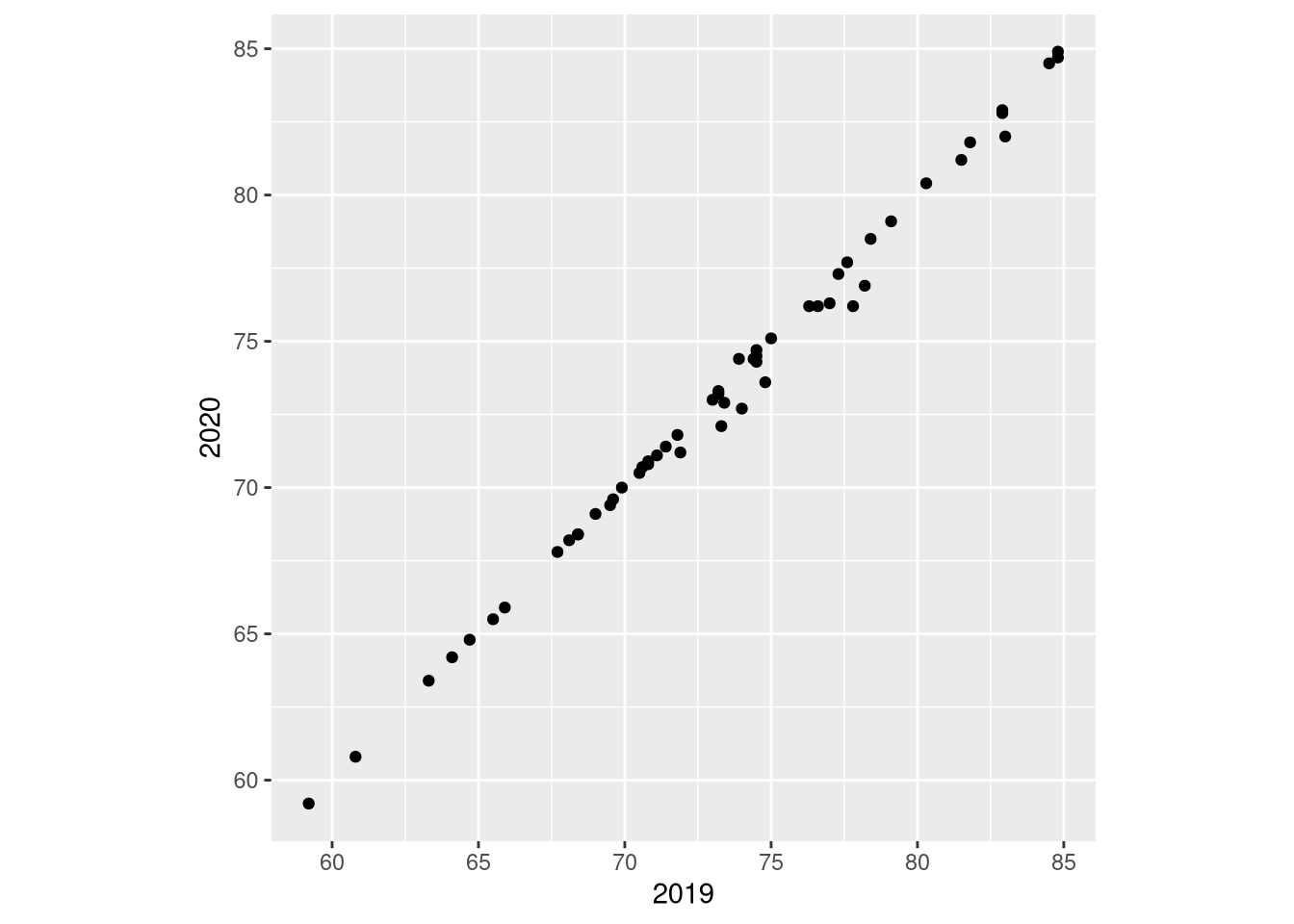
ggplot(df1sel_1920_2, aes(x = `2019`, y = `2020`)) +
    geom_point()
ggplot(df1sel_1920_2, aes(x = `2019`, y = `2020`)) +
    geom_point() +
    coord_equal()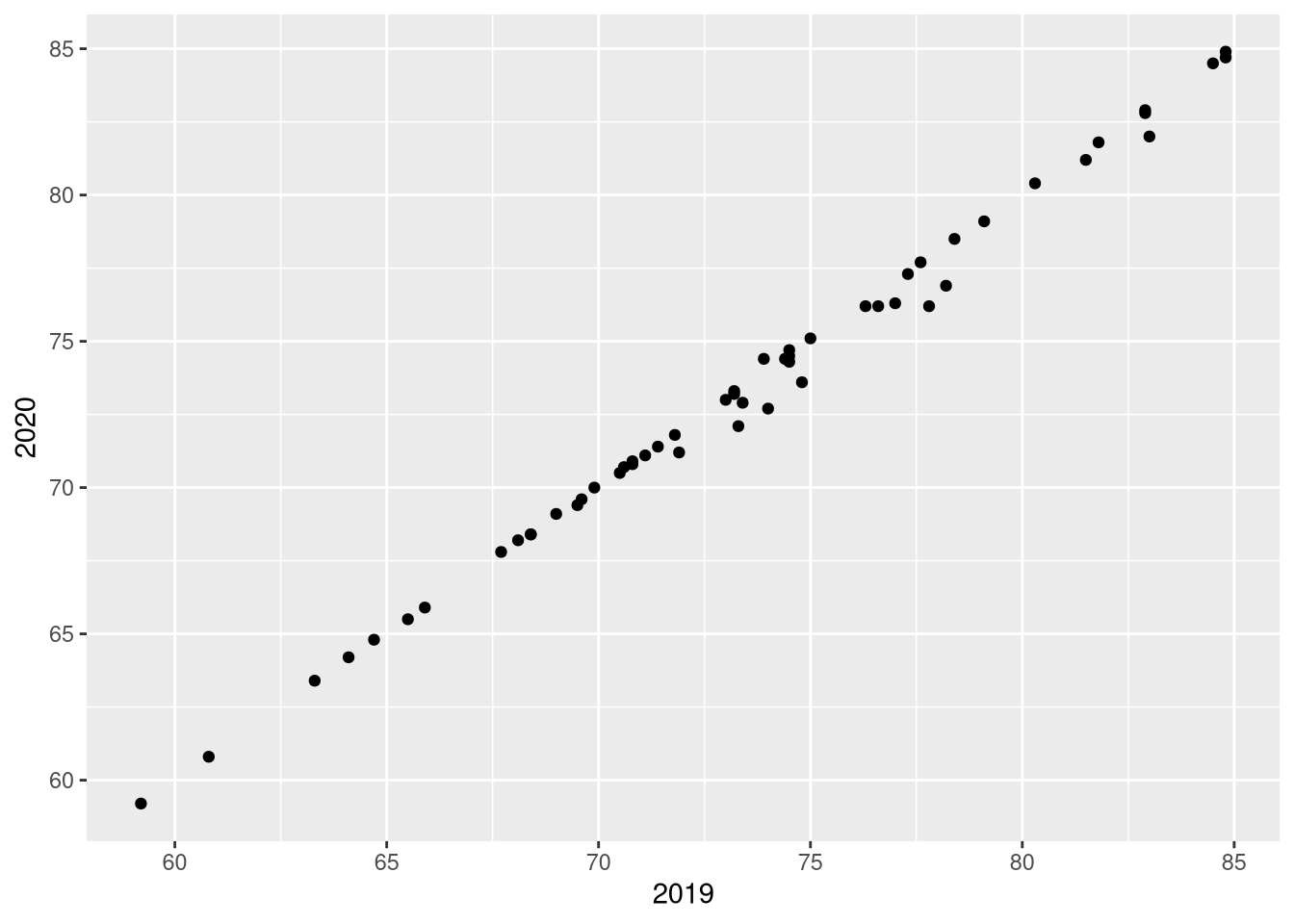 

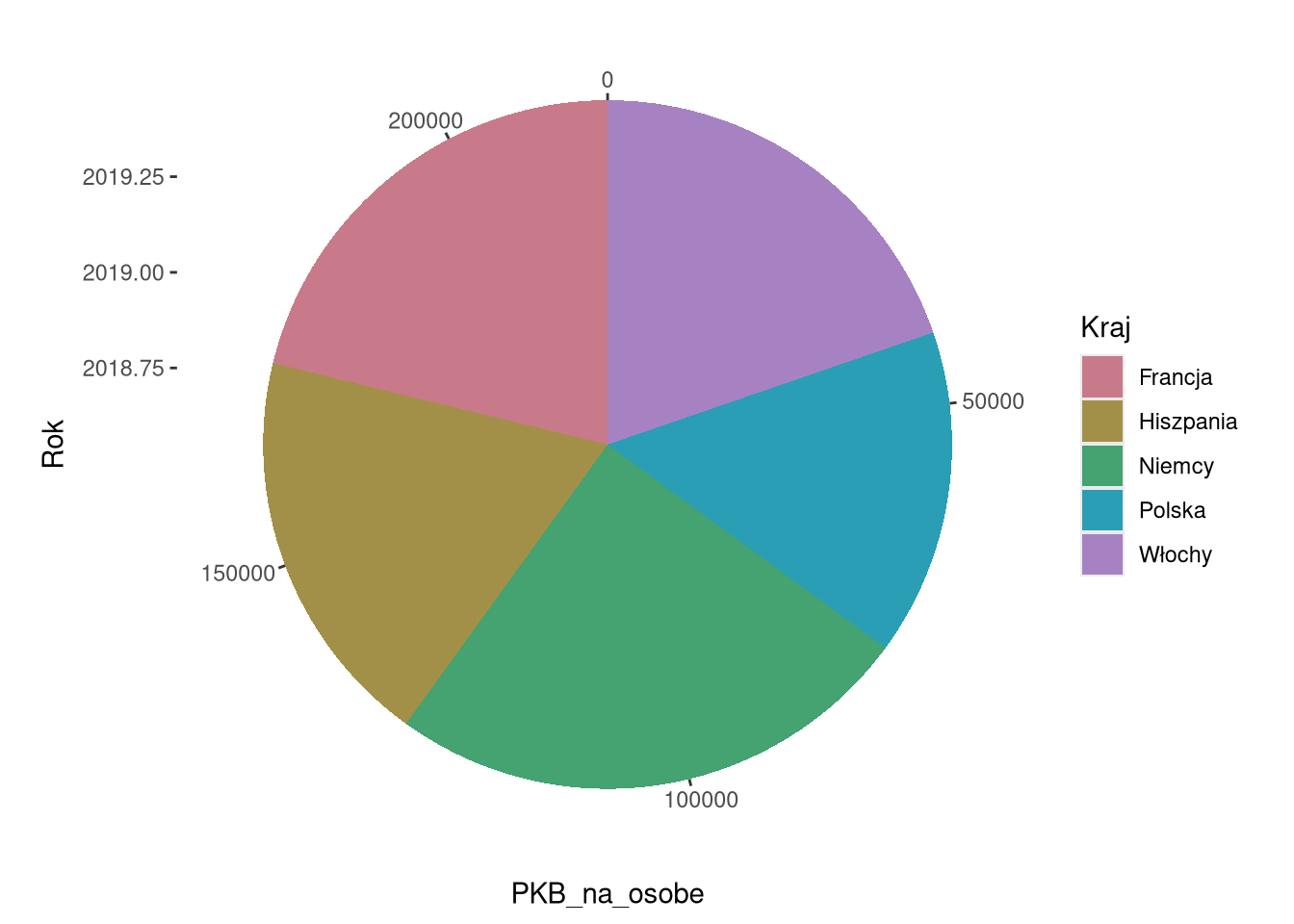
Ciekawym przykładem jest wykres kołowy – to wykres słupkowy w układzie współrzędnych biegunowych w gramatyce grafiki.

df1sel19 = filter(df1sel, Rok == 2019)
ggplot(df1sel19, aes(as.factor(Rok), PKB_na_osobe, fill = Kraj)) + 
    geom_col(position = "fill") +
    scale_fill_discrete_qualitative(palette = "Dark2")
ggplot(df1sel19, aes(Rok, PKB_na_osobe, fill = Kraj)) + 
    geom_col() +
    scale_fill_discrete_qualitative(palette = "Dark2") +
    coord_radial("y", expand = FALSE)

Układ współrzędnych biegunowych można także zastosować do innych wykresów, np. do wykresu punktowego.

ggplot(df0_2019, aes(x = PKB_na_osobe, y = Ocz_dl_zycia)) +
    geom_point() +
    coord_radial()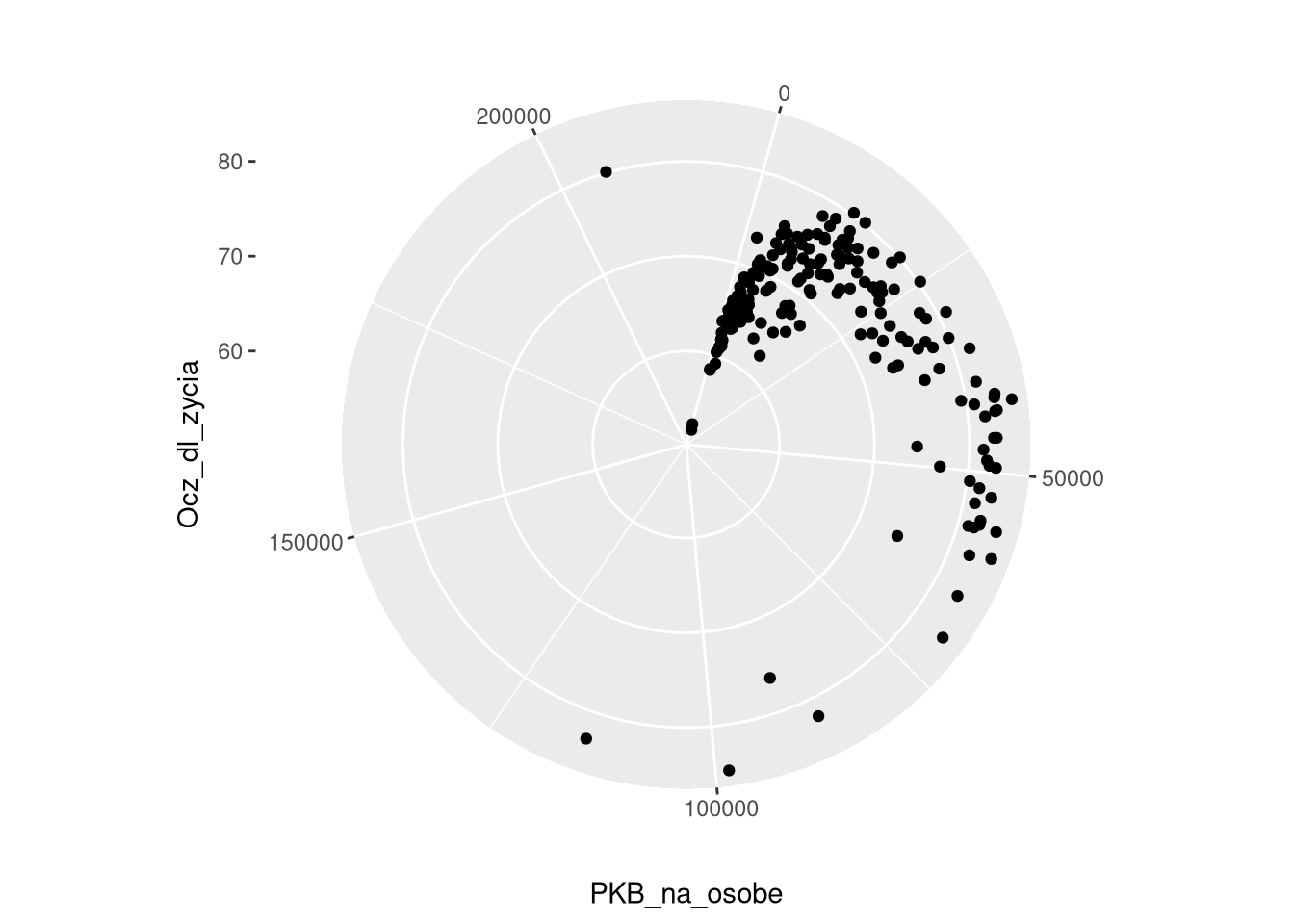

5.4.6 Warstwy

Jak ułożone będą warstwy tworzące wykres?

Wykresy mogą składać się z wielu warstw, które są nakładane na siebie. Każda kolejna warstwa jest nakładana na poprzednią, co pozwala na tworzenie bardziej złożonych wykresów.

Poniżej widać przykład dwóch wykresów: pierwszy to wykres skrzypcowy, a drugi to wykres punktowy z rozrzuconymi punktami.

ggplot(df0sel, aes(Region, Ocz_dl_zycia)) + 
    geom_violin()
ggplot(df0sel, aes(Region, Ocz_dl_zycia)) + 
    geom_jitter()

Zamiast dwóch osobnych wykresów, możliwe jest przedstawienie tych obserwacji razem w postaci nałożonych na siebie warstw.

ggplot(df0sel, aes(Region, Ocz_dl_zycia)) + 
    geom_violin() +
    geom_jitter()

W tej sytuacji nałożenie wartstw na siebie pozwala na nie tylko zobaczenie rozkładu wartości (powierzchnie), ale też tego na podstawie jakiej liczby obserwacji został on określony (punkty).

Inny przyład użycia warstw to wykres punktowy z linią trendu. Sam wykres punktowy często nie pozwala na określenie przeciętnego trendu, a sama linia trendu nie pokazuje rozkładu wartości.

ggplot(df0_2019, aes(x = PKB_na_osobe, y = Ocz_dl_zycia)) +
    geom_point()
ggplot(df0_2019, aes(x = PKB_na_osobe, y = Ocz_dl_zycia)) +
    geom_smooth()

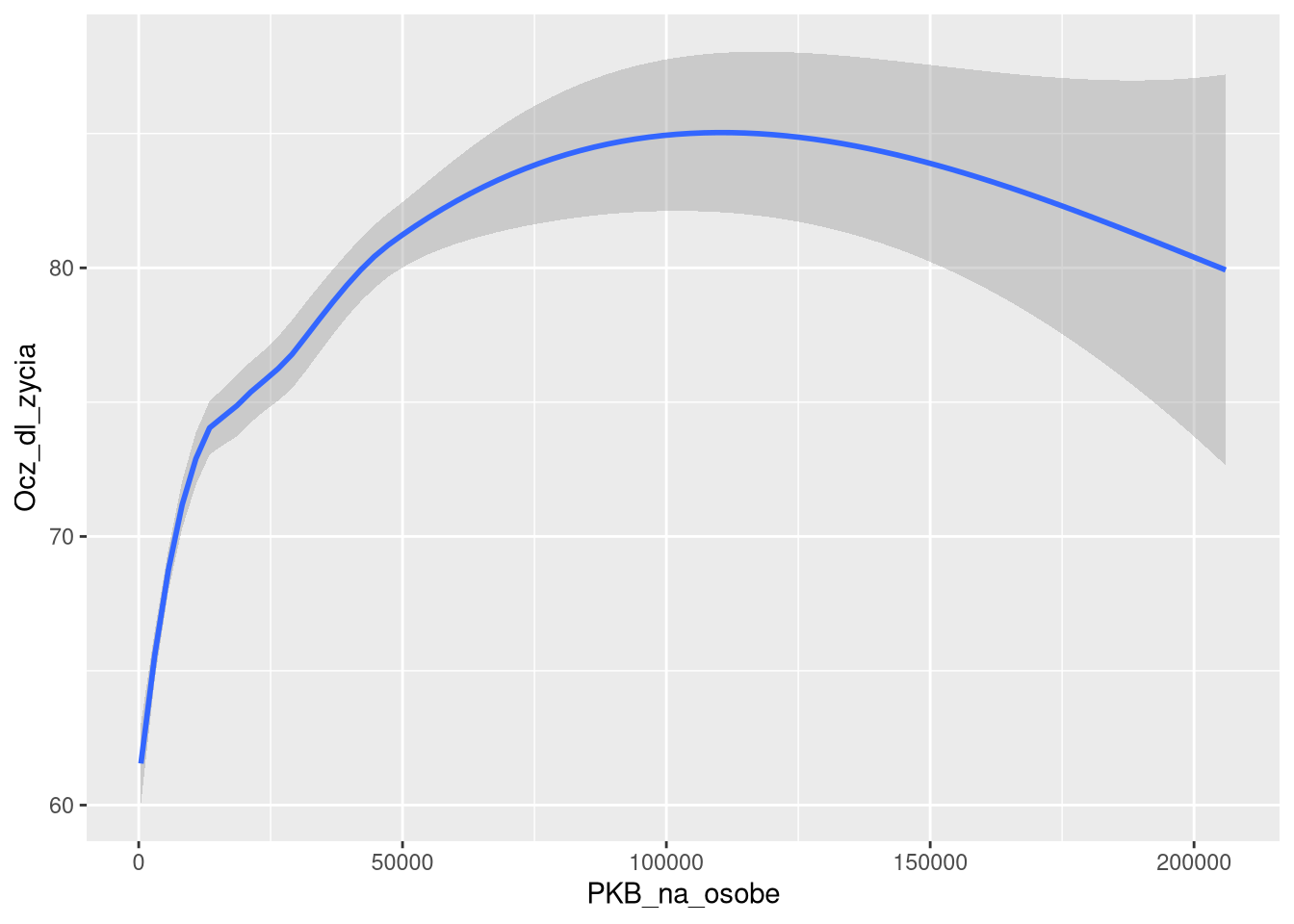
Połączenie tych dwóch warstw pozwala na zobaczenie zarówno rozkładu wartości, jak i przeciętnego trendu, co pozwala na lepsze zrozumienie badanych zależności.

ggplot(df0_2019, aes(x = PKB_na_osobe, y = Ocz_dl_zycia)) +
    geom_point() +
    geom_smooth()

5.4.7 Panele

Jak podzielić dane na wiele podwykresów?

Poniższy wykres przedstawia dane dla różncych regionów na jednym wykresie.

ggplot(df0_2019, aes(PKB_na_osobe, Ocz_dl_zycia, color = Region)) + geom_point()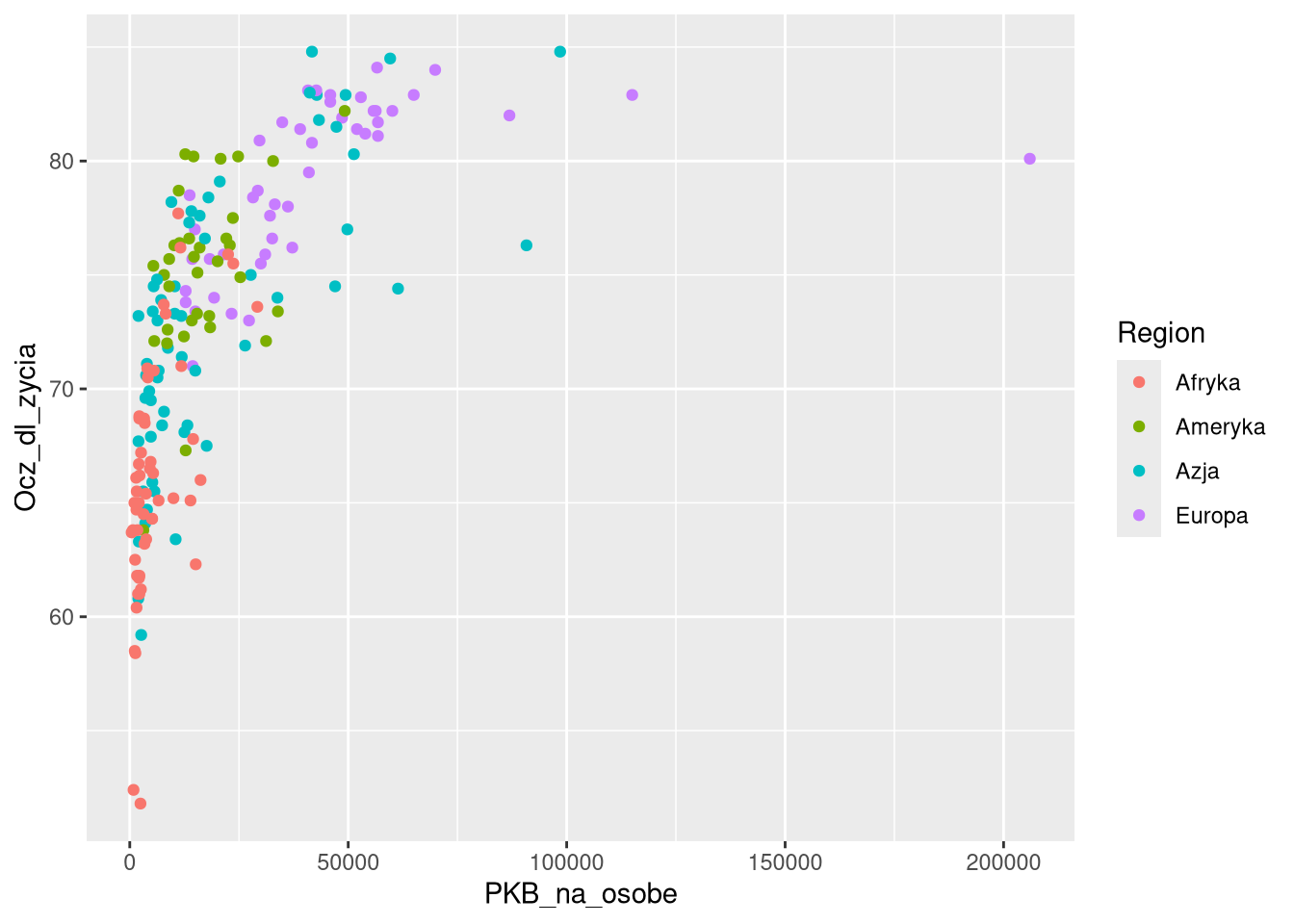

Czasem warto jednak rozważyć podzielenie danych na wiele podwykresów, co pozwala na lepsze zrozumienie rozkładu wartości dla poszczególnych kategorii.

ggplot(df0_2019, aes(PKB_na_osobe, Ocz_dl_zycia, color = Region)) + 
    geom_point() + 
    facet_wrap(~Region, drop = FALSE)

Trudno na powyższym wykresie jednak zobaczyć jak dana kategoria odnosi się do reszty obserwacji. W tym może pomóc dodanie punktów dla wszystkich obserwacji, ale w szarym kolorze jako wczesniejsza warstwa.

ggplot(df0_2019, aes(PKB_na_osobe, Ocz_dl_zycia)) + 
    geom_point(data = select(df0_2019, -Region), color = "grey") + 
    geom_point(aes(color = Region), size = 3) + 
    facet_wrap(~Region)

Wcześniejsze podwykresy były stworzone na podstawie jednej zmiennej. Możliwe jest także stworzenie podwykresów na podstawie dwóch zmiennych, co widać poniżej dla danych z lat 2000 i 2020.

df0_1920 = filter(gm0, Rok %in% c(2000, 2020))
ggplot(df0_1920, aes(PKB_na_osobe, Ocz_dl_zycia, color = Region)) + 
    geom_point() + 
    facet_grid(Region~Rok)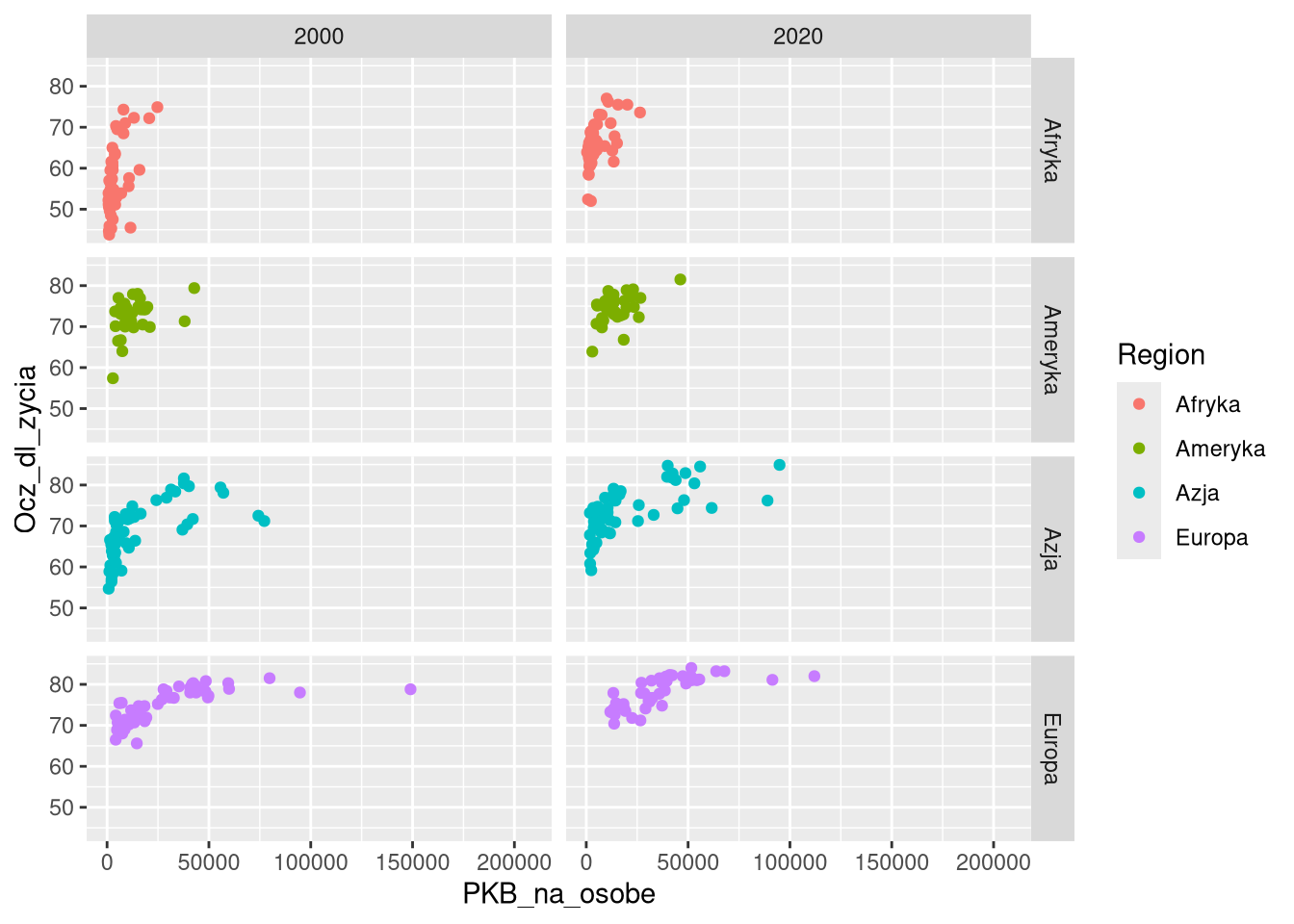

5.4.8 Dekoracje

Jaki chcemy nadać wykresowi styl?

Każda implementacja gramatyki grafiki ma wbudowany szereg domyślnych wartości, w tym takich, które określają wygląd wykresu. Przykładowo, domyślnie wykresy w ggplot2 mają szare tło i białe linie.

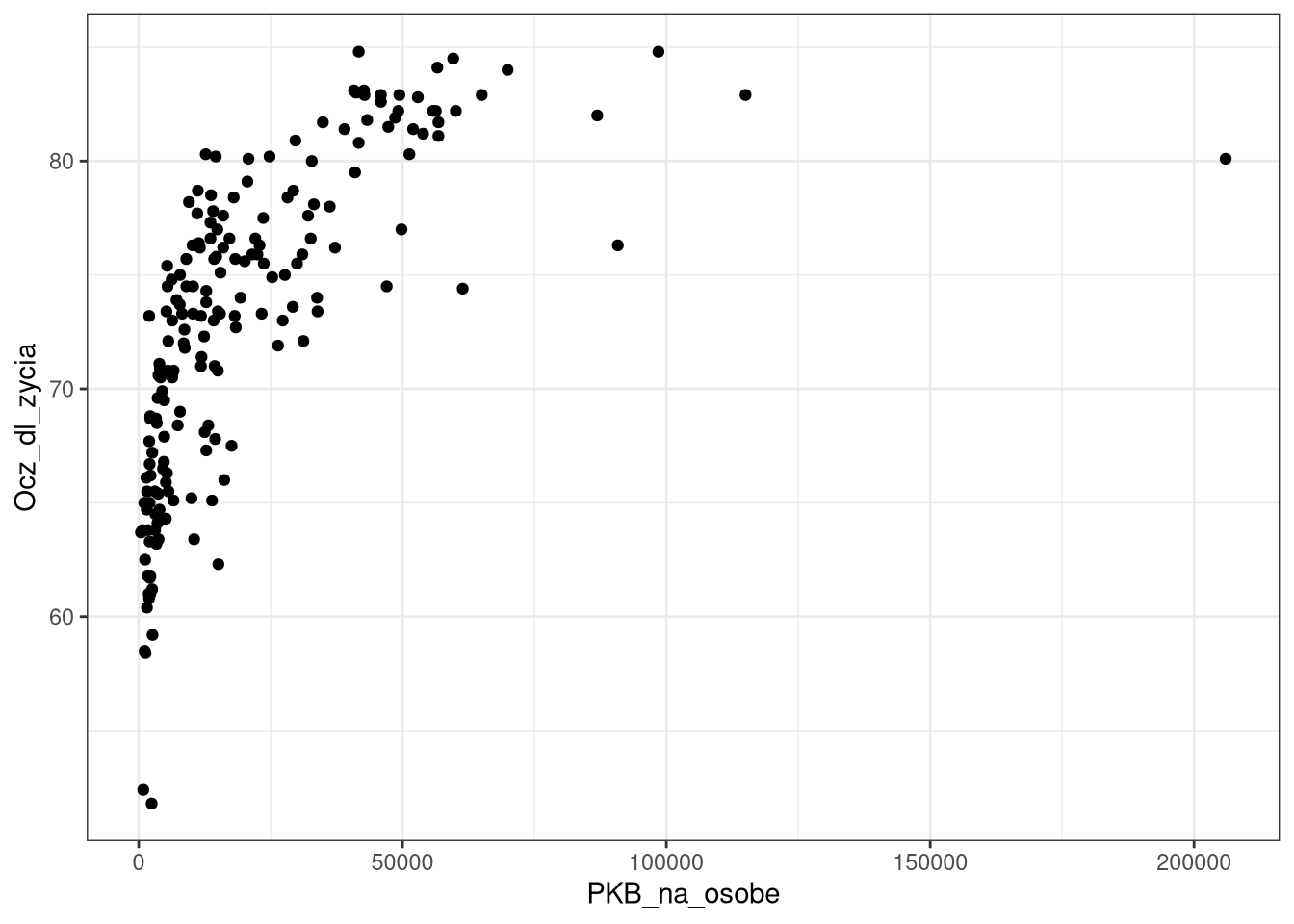
ggplot(df0_2019, aes(PKB_na_osobe, Ocz_dl_zycia)) + 
    geom_point()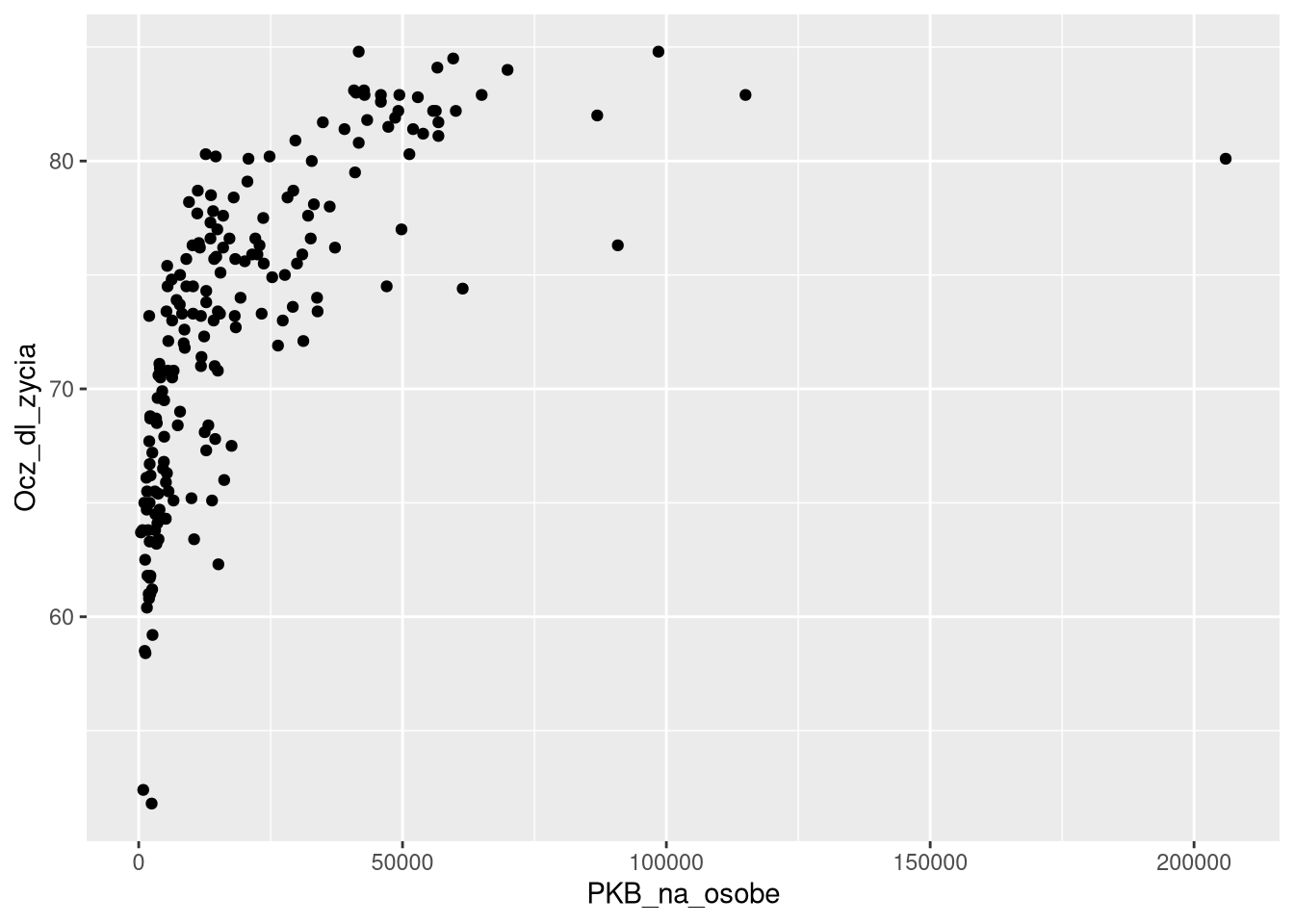

Możliwe jest jednak modyfikowanie tych wartości. Najprostszym sposobem jest użycie gotowych dektoracji (ang., theme), które zmieniają wygląd wykresu.

ggplot(df0_2019, aes(PKB_na_osobe, Ocz_dl_zycia)) + 
    geom_point() +
    theme_bw()
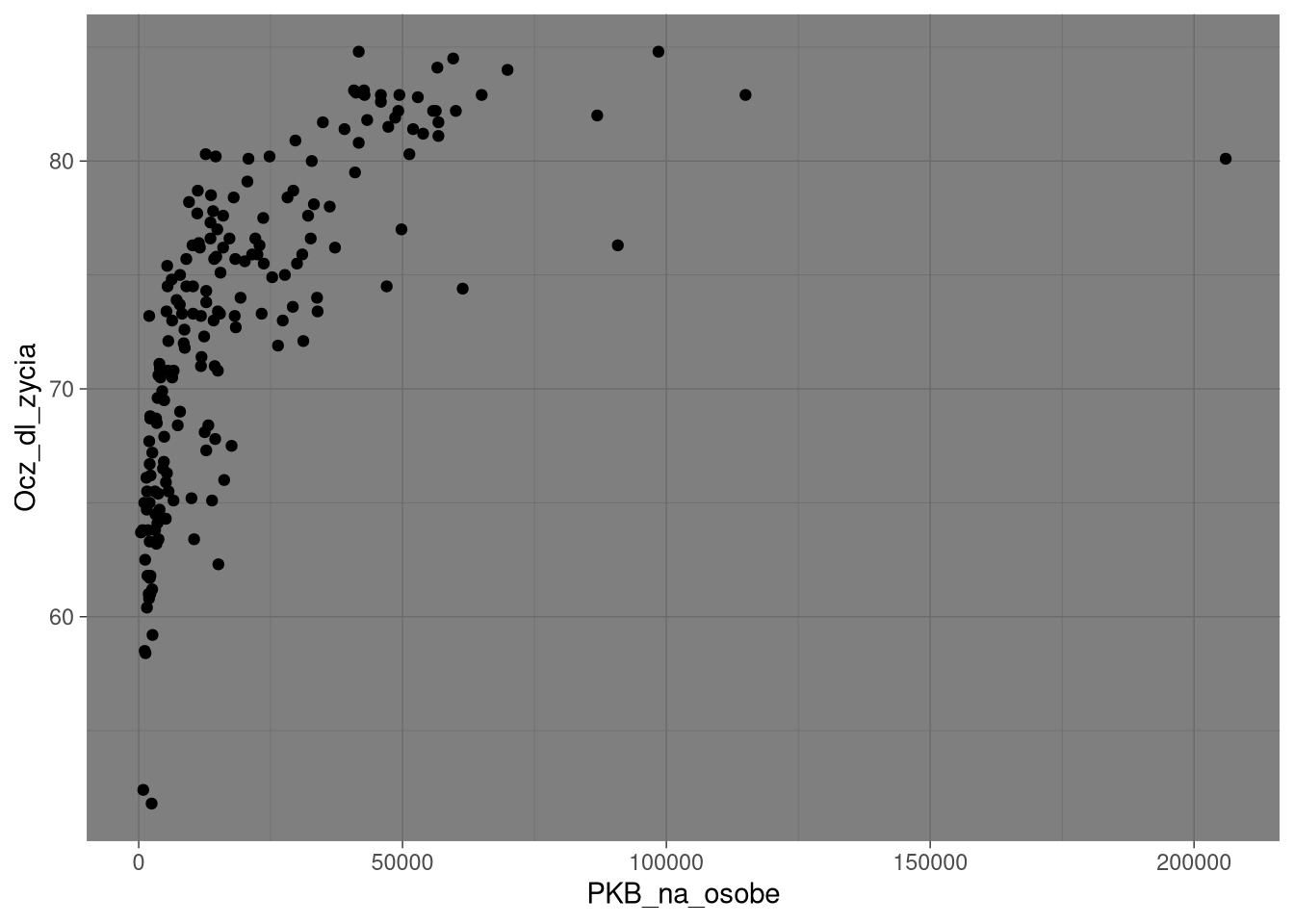
ggplot(df0_2019, aes(PKB_na_osobe, Ocz_dl_zycia)) + 
    geom_point() +
    theme_dark()
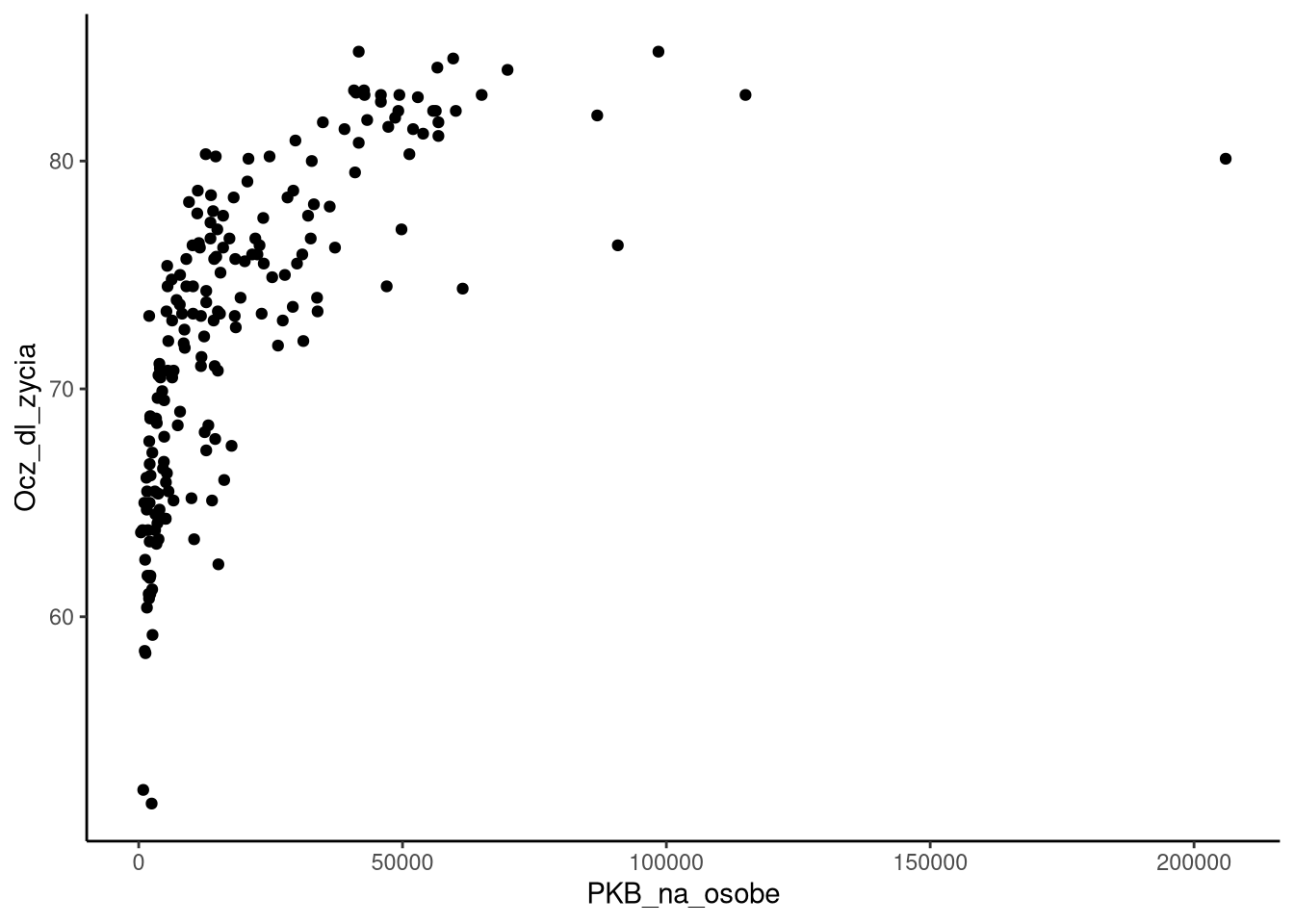
ggplot(df0_2019, aes(PKB_na_osobe, Ocz_dl_zycia)) + 
    geom_point() +
    theme_classic()
ggplot(df0_2019, aes(PKB_na_osobe, Ocz_dl_zycia)) + 
    geom_point() +
    theme_void()

Bertin, Jacques. 1983. „Semiology of graphics: diagrams”. Networks, Maps 10 (00690805.1987): 10438353.

Biecek, Przemyslaw. 2016. Odkrywać! Ujawniać! Objaśniać! Zbiór esejów o sztuce przedstawiania danych. Fundacja Naukowa SmarterPoland.pl.

Wickham, Hadley. 2010. „A Layered Grammar of Graphics”. Journal of Computational and Graphical Statistics 19 (1): 3–28. https://doi.org/10.1198/jcgs.2009.07098.

Wilkinson, Leland. 2005. The Grammar of Graphics. Springer.